Question

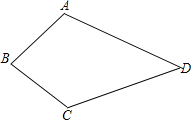
【题目】（A类）已知如图，四边形ABCD中，AB=BC，AD=CD，求证：∠A=∠C．

（B类）已知如图，四边形ABCD中，AB=BC，∠A=∠C，求证：AD=CD．

Answer 1

【答案】（A类）证明见解析；（B类）证明见解析.

【解析】

（A类）连接AC，由AB=AC、AD=CD知∠BAC=∠BCA、∠DAC=∠DCA，两等式相加即可得；

（B类）连接AC，由AB=BC，可得∠BAC=∠BCA，再根据∠BAD=∠BCD则可得∠DAC=∠DCA，根据等腰三角形的判定即可得AD＝CD.

（A类）连接AC，

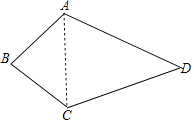
∵AB=AC，AD=CD，

∴∠BAC=∠BCA，∠DAC=∠DCA，

∴∠BAC+∠DAC=∠BCA+∠DCA，

即∠BAD=∠BCD；

（B类）连接AC，

∵AB=BC，

∴∠BAC=∠BCA，

又∵∠BAD=∠BCD，即∠BAC+∠DAC=∠BCA+∠DCA，

∴∠DAC=∠DCA，

∴AD=CD．