Question

【题目】如图，在正方形中，点是上一动点（不与，重合），对角线、相交于点，过点分别作、的垂线，分别交、于点、，交、于点、．下列结论：①；②；③；④；⑤当时，点是的中点．

其中正确的结论有_____．

Answer 1

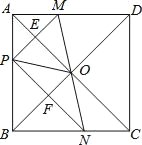
【答案】①②③⑤

【解析】

①根据正方形的每一条对角线平分一组对角可得∠PAE=∠MAE=45°，然后利用“角边角”证明△APE和△AME全等；
②根据全等三角形对应边相等可得PE=EM=PM，同理，FP=FN=NP，证出四边形PEOF是矩形，得出PF=OE，证得△APE为等腰直角三角形，得出AE=PE，PE+PF=OA，即可得到PM+PN=AC；
③根据矩形的性质可得PF=OE，再利用勾股定理即可得到PE2+PF2=PO2；
④判断出△POF不一定等腰直角三角形，△BNF是等腰直角三角形，从而确定出两三角形不一定相似；
⑤证出△APM和△BPN以及△APE、△BPF都是等腰直角三角形，从而得出结论．

解：①∵四边形是正方形，

∴，

∵，

∴，

在和中，

，

∴，

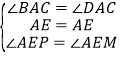故①正确；

②∵，

∴，

同理，，

∵正方形中，，

又∵，，

∴，且中，

∴四边形是矩形．

∴，

∵在中，，，

∴为等腰直角三角形，

∴，

∴，

又∵，，，

∴，

故②正确；

③∵四边形是矩形，

∴，

在直角中，，

∴，

故③正确；

④∵，

∴.

是等腰直角三角形，而不一定是，

∴与不一定相似，

故④错误；

⑤∵，

∴，

∴是等腰直角三角形，

同理，是等腰直角三角形，

当时，是等腰直角三角形．

∴，

又∵和都是等腰直角三角形，

∴，即是的中点，

故⑤正确；

故答案为：①②③⑤．