��Ŀ����
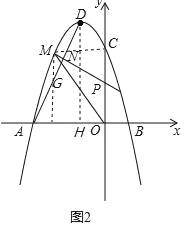
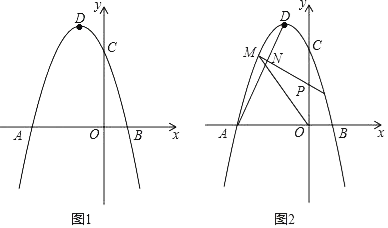
����Ŀ����ͼ�������ߵĶ���D������Ϊ����1��4������������x���ཻ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C��0��3����
��1���������ߵı���ʽ��
��2����ͼ1����֪��E��0����3�����������ߵĶԳ������Ƿ����һ��F��ʹ����CEF���ܳ���С��������ڣ������F�����ꣻ��������ڣ���˵�����ɣ�
��3����ͼ2������AD������P���߶�OC�ϵ�һ���㣬����P���߶�AD�Ĵ��ߣ��ڵڶ����ֱ��������ߡ��߶�AD�ཻ�ڵ�M��N����MN���ʱ������POM�������
���𰸡�(1)y=��x2��2x+3��(2) ����, F����1��0��,���ɼ���������3��2
��������
(1)���ݶ���ʽ����������ߵı���ʽ;
(2) ��ͼ 1���� C���ڶԳ���ĶԳƵ� C�䣬����EC�佻�Գ����� F��������ԳƵ����·������, CF+EF��ֵ��С�����CEF���ܳ���С;
(3)��ͼ2,�����ô���ϵ������AD�Ľ���ʽΪ: y��2x+6,��M��m����m2��2m+3������G��m��2m+6��������3��m�ܩ�1��,֤����MNG�ס�AHD,�б���ʽ�ɵ�MN�ı���ʽ,�����䷽���ɵõ�m=-2ʱ,MN�����ֵ,֤����MCP�ס�DHA,ͬ����PC�ij�,�Ӷ���OP�ij�,���������ε������ʽ�ɵý���,����m=-2������㼴��
��1���������ߵı���ʽΪ��y��a��x+1��2+4��
��x��0��y��3����ã�3��a��0+1��2+4����ã�a����1
�������ߵı���ʽΪy������x+1��2+4����x2��2x+3��
��2�����ڣ���ͼ 1���� C���ڶԳ���ĶԳƵ� C�䣬����EC�佻�Գ����� F����ʱ CF+EF��ֵ��С�����CEF���ܳ���С��
��C��0��3����
��C�䣨��2��3������C��E�Ľ���ʽΪ��y����3x��3��
��x����1ʱ��y����3������1����3��0��
��F����1��0��
��3����ͼ2����A����3��0����D����1��4����
��AD�Ľ���ʽΪ��y��2x+6��
����D��DH��x����H������M��MG��x�ύAD��G��
AH����1������3����2��DH��4����AD��![]() ��
��
��M��m����m2��2m+3������G��m��2m+6��������3��m�ܩ�1����
��MG������m2��2m+3������2m+6������m2��4m��3��
������֪��MNG�ס�AHD��
��![]()
��![]()
��![]()
�൱m����2ʱ��MN�����ֵ��
��ʱM����2��3�����֡�C��0��3��������MC
��MC��y��
�ߡ�CPM����HAD����MCP����DHA��90�㣬
���MCP�ס�DHA��
��![]()
�� ![]()
��PC��1
��OP��OC��PG��3��1��2��
��S��POM��![]() ��2��
��2��