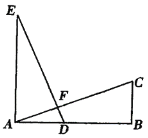
题目内容
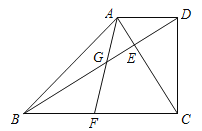
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,有一动点
,有一动点![]() 以
以![]() 的速度沿
的速度沿![]() 的路径运动,设
的路径运动,设![]() 点运动的时间为
点运动的时间为![]() ,
,![]() 的面积为
的面积为![]()
![]() .
.
![]() 当
当![]() 是等腰直角三角形时,直接写出
是等腰直角三角形时,直接写出![]() 的值.答:
的值.答:![]() ________;
________;
![]() 求
求![]() 与
与![]() 的函数关系式并写出自变量
的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积为
的面积为![]() .
.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() (
(![]() ),
),![]() (
(![]() ),
),![]() (
(![]() );(3)当
);(3)当![]() 为
为![]() 或
或![]() 时,
时,![]() 的面积为
的面积为![]() .
.
【解析】
(1)当点P运动到B点和C点时,△ADP是等腰直角三角形,然后写出对应的t的值;
(2)分类讨论:当点P在AB上运动或点P在BC上运动或点P在CD上运动时,分别写出对应的t的取值范围,然后根据三角形面积公式求出对应的S;
(3)利用(2)中S与t的函数关系式,求函数值为12时所对应的t的值即可.
(1)当t=8s或16s时,△ADP是等腰直角三角形;
故答案为8s或16s;
![]() 当
当![]() 时,如图
时,如图![]() ,
,
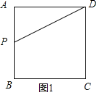
![]() ;
;
当![]() 时,如图
时,如图![]() ,
,
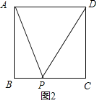 ;
;
当![]() 时,如图
时,如图![]() ,
,
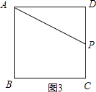
![]() ;
;
![]() 当
当![]() 时,解得
时,解得![]() ;
;
当![]() 时,解得
时,解得![]() ,
,
所以当![]() 为
为![]() 或
或![]() 时,
时,![]() 的面积为
的面积为![]() .
.

练习册系列答案
相关题目
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
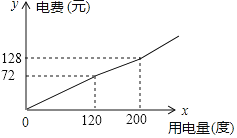
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?