Question

【题目】如图1，在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，点的坐标为，将直线沿轴向上平移4个单位长度后恰好经过两点。

（1）求直线及抛物线的解析式；

（2）将直线沿轴向上平移5个单位长度后与抛物线交于两点，若点是抛物线位于直线下方的一个动点，连接，交直线于点，连接和。设的面积为，当S取得最大值时，求出此时点的坐标及的最大值；

（3）如图2，记（2）问中直线与轴交于点，现有一点从点出发，先沿轴到达点，再沿到达点，已知点在轴上运动的速度是每秒2个单位长度，它在直线上运动速度是1个单位长度。现要使点按照上述要求到达点所用的时间最短，请简述确定点位置的过程，求出点的坐标，不要求证明。

Answer 1

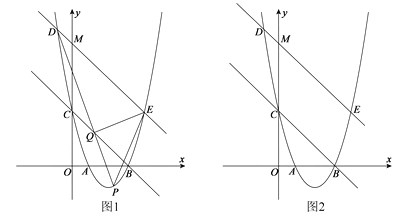
【答案】（1）直线BC的解析式为y=-x+4，抛物线的解析式为y=x2-5x+4．（2）△PQE的面积最大值为12．此时P（2，-2）；（3）K（，0）．