��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�ڣ������������Ͷ��κ���y=k��x2+x��1����ͼ���ڵ�A��1��k���͵�B����1����k����
��1����k=��2ʱ�����������Ľ���ʽ��
��2��Ҫʹ�����������Ͷ��κ�������y����x�������������kӦ����������Լ�x��ȡֵ��Χ��
��3������κ�����ͼ��Ķ���ΪQ������ABQ����ABΪб�ߵ�ֱ��������ʱ����k��ֵ��
��4����CΪx����һ���㣬��C������Ϊ��2k��0��������ABC����ABΪб�ߵ�ֱ��������ʱ����K��ֵ��
���𰸡�
��1��
�⣺��k=��2ʱ��A��1����2����
��A�ڷ���������ͼ���ϣ�
���跴���������Ľ���ʽΪ��y= ![]() ��
��
����A��1����2�����2= ![]() ��
��
��ã�m=��2��
�෴���������Ľ���ʽΪ��y=�� ![]()
��2��
�⣺��Ҫʹ�����������Ͷ��κ�������y����x�����������
��k��0��
�߶��κ���y=k��x2+x��1��=k��x+ ![]() ��2��
��2�� ![]() k���Գ���Ϊ��ֱ��x=��
k���Գ���Ϊ��ֱ��x=�� ![]() ��
��
Ҫʹ���κ���y=k��x2+x��1������������������k��0������£�x�����ڶԳ������ߣ�
��x���� ![]() ʱ������ʹ��y����x�����������
ʱ������ʹ��y����x�����������
������������k��0��x���� ![]()
��3��
�⣺����һ��
�ɣ�2���ɵã�Q���� ![]() ����
���� ![]() k����
k����
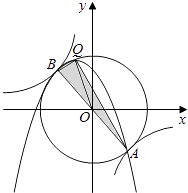
�ߡ�ABQ����ABΪб�ߵ�ֱ�������Σ�A����B�����ԭ��Գƣ�
��ԭ��Oƽ��AB��
��OQ=OA=OB��
��BD��OC��QC��OC��

��OQ= ![]() =
= ![]() ��
��
��OB= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�k=�� ![]()
![]() ��
��
��������
�����ߵĶ���Q���� ![]() ����
���� ![]() k����A��1��k����B����1����k����
k����A��1��k����B����1����k����
�ߡ�ABQ����ABΪб�ߵ�ֱ�������Σ�
��AQ��BQ��
��KAQ��KBQ=��1��
�� 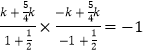 ��
��
�� ![]() ��
��
k1= ![]() ��k2=��
��k2=�� ![]() ��
��
��4��
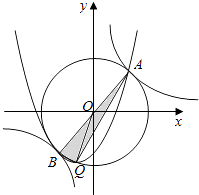
��ABC����ABΪб�ߵ�ֱ�������Σ�
��AC��BC��
��KAC��KBC=��1��
��A��1��k����B����1����k����C��2k��0����
�� ![]() ��
��
��3k2=1��
��k1= ![]() ��k2=��
��k2=�� ![]() ��
��
������������һ����1����k=��2ʱ��������õ�A�����꣬Ȼ���跴���������Ľ���ʽΪ��y= ![]() �����ô���ϵ����������ô𰸣���2���ɷ����������Ͷ��κ�������y����x����������ɵ�k��0�����ɶ��κ���y=k��x2+x��1���ĶԳ���Ϊx=��
�����ô���ϵ����������ô𰸣���2���ɷ����������Ͷ��κ�������y����x����������ɵ�k��0�����ɶ��κ���y=k��x2+x��1���ĶԳ���Ϊx=�� ![]() ���ɵ�x����
���ɵ�x���� ![]() ʱ������ʹ��y����x�����������3���ɡ�ABQ����ABΪб�ߵ�ֱ�������Σ�A����B�����ԭ��Գƣ�����ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬���ɵ�OQ=OA=OB������Q����
ʱ������ʹ��y����x�����������3���ɡ�ABQ����ABΪб�ߵ�ֱ�������Σ�A����B�����ԭ��Գƣ�����ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬���ɵ�OQ=OA=OB������Q���� ![]() ����
���� ![]() k����A��1��k�������ɵ�
k����A��1��k�������ɵ� ![]() =
= ![]() ���̶���ô𰸣�����������1���ԣ���2�����ݷ��������������κ����������Եó�k��x��ȡֵ��Χ����3�������Q�����꣬����ABΪб�ߣ��ó�AQ��ֱBQ�����ûƽ������ʽ�����⣮��4���г�A��B��C����������꣬���ûƽ������ʽ�����⣮
���̶���ô𰸣�����������1���ԣ���2�����ݷ��������������κ����������Եó�k��x��ȡֵ��Χ����3�������Q�����꣬����ABΪб�ߣ��ó�AQ��ֱBQ�����ûƽ������ʽ�����⣮��4���г�A��B��C����������꣬���ûƽ������ʽ�����⣮
�����㾫����������Ҫ�����˷��������������ʺͶ��κ��������ʵ����֪ʶ�㣬��Ҫ��������:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ����������������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�