题目内容
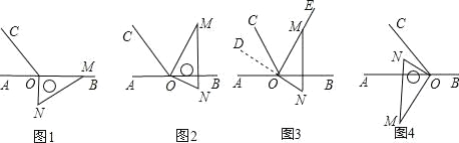
【题目】已知,在下列各图中,点 O 为直线 AB 上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
(1)如图 1,三角板一边 OM在射线 OB 上,另一边 ON在直线 AB的下方,求∠BOC的度数,∠CON 的度数;
(2)如图 2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线 AB的下方,求此时∠BON 的度数;
(3)请从下列(A),(B)两题中任选一题作答. 我选择哪一题.
(A)在图 2 中,延长线段 NO 得到射线 OD,如图 3,求∠AOD 的度数;写出∠DOC 与∠BON 的数量关系;
(B)如图 4,MN⊥AB,ON 在∠AOC 的内部,若另一边 OM 在直线 AB 的下方, 求∠COM+∠AON 的度数;∠AOM﹣∠CON 的度数.
【答案】(1)120;150;(2)30°;(3)A(或 B);(A)30;∠DOC=∠BON;(B)150;30.
【解析】
(1)利用两角互补,即可得出结论;
(2)根据OM平分∠BOC,可得出∠BOM=60°,由∠MON=∠BOM+∠BON=90°可求得∠BON的度数;
(3)根据直角三角板MON各角的度数以及图中各角的关系即能得出结论.
(1)∵∠AOC=60°,∠BOC 与∠AOC 互补,∠AON=90°
∴∠BOC=180°﹣60°=120°,∠CON=∠AOC+∠AON=60°+90°=150°.
(2)∵三角板一边 OM 恰好在∠BOC 的角平分线 OE 上,∠BOC=120°,
∴∠BOM= ![]() ∠BOC=60°,
∠BOC=60°,
又∵∠MON=∠BOM+∠BON=90°,
∴∠BON=90°﹣60°=30°.
(3)(A)∵∠AOD=∠BON(对顶角),∠BON=30°,
∴∠AOD=30°, 又∵∠AOC=60°,
∴∠DOC=∠AOC﹣∠AOD=60°﹣30°=30°=∠BON.
(B)∵MN⊥AB,
∴∠AON 与∠MNO 互余,
∵∠MNO=60°(三角板里面的 60°角),
∴∠AON=90°﹣60°=30°,
∵∠AOC=60°,150
∴∠CON=∠AOC﹣∠AON=60°﹣30°=30°,
∴∠COM+∠AON=∠MON+2∠CON=90°+2×30°=150°,
∠AOM﹣∠CON=∠MON﹣2∠CON=90°﹣2×30°=30°.

【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?



