题目内容
【题目】如图,在△ABC中,BA=BC,∠B=120°,线段AB的垂直平分线MN交AC于点D,且AD=8cm.求:
(1)∠ADG的度数;
(2)线段DC的长度.
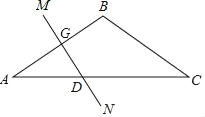
【答案】(1)∠ADG=60°;(2)DC=16cm.
【解析】
(1)根据等腰三角形的两个底角相等、三角形内角和定理来求∠A的度数;
(2)连接BD.根据线段垂直平分线的性质知△ABD是等腰三角形;然后利用(1)中的∠A=∠C=30°和已知条件∠B=120°可以推知△CDB是直角三角形,利用30度角所对的直角边是斜边的一半即可求得BD与CD间的数量关系;最后利用等腰三角形ABD的两腰相等(AD=BD)通过等量代换即可求得CD=2AD,从而求得线段DC的长度.
(1)在△ABC中,∵BA=BC,∴∠A=∠C(等边对等角).
又∵∠B=120°,∴∠A=![]() (180°﹣120°)=30°(三角形内角和定理),∴∠ADG=90°﹣30°=60°.
(180°﹣120°)=30°(三角形内角和定理),∴∠ADG=90°﹣30°=60°.
(2)连接BD.
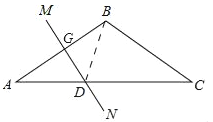
∵AB的垂直平分线DG交AC于点D,∴AD=BD,∠A=∠ABD=30°,∴∠CBD=90°.
由(1)知∠A=∠C=30°,∴BD=![]() CD(30°所对的直角边是斜边的一半),∴CD=2AD=2BD.
CD(30°所对的直角边是斜边的一半),∴CD=2AD=2BD.
又∵AD=8cm,∴DC=16cm.

练习册系列答案
相关题目
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?


