题目内容
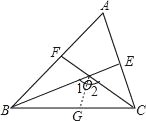
【题目】△ABC中,∠A=60°,平分线BE、CF相交于O,求证:OE=OF.

【答案】见解析
【解析】
由∠A=60°,BE、CF是角平分线就可以得出∠BOC=120,进而得出∠BOF=∠COE=60°,在BC上取点G,使BG=BF,就可以得出△BOF≌△BOG,就可以得出OF=OG,∠BOF=∠1=60°,进而求出∠2=60°,得出∠2=∠COE,得出△COE≌△COG,就有OE=OG,进而得出结论.
在BC上取点G,使BG=BF,
∵BE平分∠ABC,CF∠ACB,
∴∠ABE=∠CBE=![]() ∠ABC,∠ACF=∠BCF=
∠ABC,∠ACF=∠BCF=![]() ∠ACB,
∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴![]() ∠ABC+
∠ABC+![]() ∠ACB=60°,
∠ACB=60°,
∴∠BOC=120°,
∴∠BOF=∠COE=60°,
在△BOF和△BOG中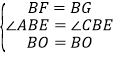 ,
,
∴△BOF≌△BOG(SAS),
∴OF=OG,∠BOF=∠1,
∴∠1=60°,
∴∠2=60°,
∴∠2=∠COE,
在△COE和△COG中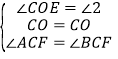 ,
,
∴△COE≌△COG(ASA),
∴OE=OG.
∴OE=EF.

练习册系列答案
相关题目