Question

【题目】如图，AB是⊙O的直径，点C、D在圆上，且四边形AOCD是平行四边形，过点D作⊙O的切线，分别交OA延长线与OC延长线于点E、F，连接BF．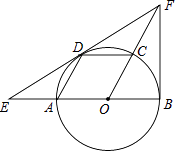

（1）求证：BF是⊙O的切线；
（2）已知圆的半径为1，求EF的长．

Answer 1

【答案】
（1）证明：连结OD，如图，∵四边形AOCD是平行四边形，

而OA=OC，

∴四边形AOCD是菱形，

∴△OAD和△OCD都是等边三角形，

∴∠AOD=∠COD=60°，

∴∠FOB=60°，

∵EF为切线，

∴OD⊥EF，

∴∠FDO=90°，

在△FDO和△FBO中

，

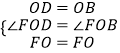∴△FDO≌△FBO，

∴∠ODF=∠OBF=90°，

∴OB⊥BF，

∴BF是⊙O的切线

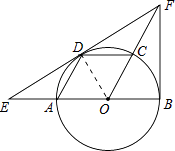
（2）解：在Rt△OBF中，∵∠FOB=60°，

而tan∠FOB= ，

∴BF=1×tan60°= ．

∵∠E=30°，

∴EF=2BF=2 ．

【解析】（1）先证明四边形AOCD是菱形，从而得到∠AOD=∠COD=60°，再根据切线的性质得∠FDO=90°，接着证明△FDO≌△FBO得到∠ODF=∠OBF=90°，然后根据切线的判定定理即可得到结论；（2）在Rt△OBF中，利用60度的正切的定义求解．本题考查了切线的判断与性质：圆的切线垂直于经过切点的半径；经过半径的外端且垂直于这条半径的直线是圆的切线．有切线时，常常“遇到切点连圆心得半径”．