题目内容
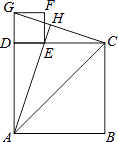
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.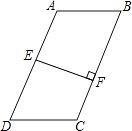
(1)若AB=DC,则四边形ABCD的面积S=;
(2)若AB>DC,则此时四边形ABCD的面积S′ S(用“>”或“=”或“<”填空).
【答案】
(1)15
(2)=
【解析】解:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
故答案为:15.
(2)如图,连接EC,延长CD、BE交于点P,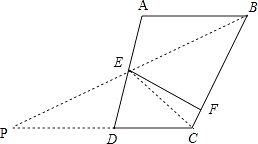
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵ 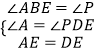 ,
,
∴△ABE≌△DPE(AAS),
∴S△ABE=S△DPE , BE=PE,
∴S△BCE=S△PCE ,
则S四边形ABCD=S△ABE+S△CDE+S△BCE
=S△PDE+S△CDE+S△BCE
=S△PCE+S△BCE
=2S△BCE
=2× ![]() ×BC×EF
×BC×EF
=15,
∴当AB>DC,则此时四边形ABCD的面积S′=S,
故答案为:=.
(1)若AB=DC,则四边形ABCD是平行四边形,据此求出它的面积是多少即可.(2)连接EC,延长CD、BE交于点P,证△ABE≌△DPE可得S△ABE=S△DPE、BE=PE,由三角形中线性质可知S△BCE=S△PCE , 最后结合S四边形ABCD=S△ABE+S△CDE+S△BCE可得答案.此题主要考查了平行四边形的判定和性质的应用及全等三角形的判定与性质,通过构建全等三角形将梯形面积转化为三角形面积去求是解题的关键.

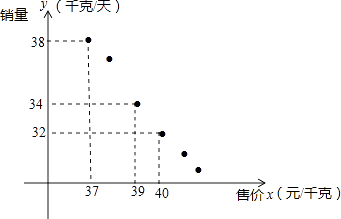
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且 ![]() =8,S乙2=1.8,根据上述信息完成下列问题:
=8,S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是 , 中位数是 .
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.