Question

【题目】材料：对于平面直角坐标系中的任意两点，，我们把叫做，两点间的距离公式，记作，如：，，则，两点的距离为

请根据以上的阅读材料，解答下列问题：

（1）当，的距离，求出的值．

（2）若在平面内有一点，使有最小值，求出它最小值和此时的范围．

（3）若有最小值，请直接写出最小值．

Answer 1

【答案】（1）a=3或-5；（2）-4≤x0≤2；（3）2+4．

【解析】

（1）根据两点间距离公式构建方程即可解决问题．
（2）求的最小值，相当于求点（x0，y0）到点（-4，4）和点（2，4）的距离和的最小值．
（3）由，当2x=3y时，这个式子有最小值，最小值为2，因为=，求出的最小值即可解决问题．

（1）由题意：（a+1）2+（1-4）2=52，
解答a=3或-5．
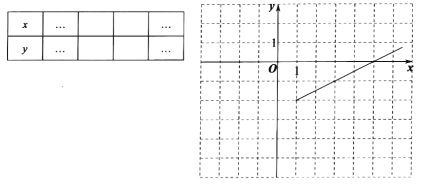
（2）求的最小值，相当于求点（x0，y0）到点（-4，4）和点（2，4）的距离和的最小值，观察图象可知最小值=6，此时-4≤x0≤2．
（3）∵，
∴

∵相当于求点（2x，2）到点（3y，0）的距离的最小值，

∴当2x=3y时，这个式子有最小值，最小值为2，

求=相当于求点（2x，2）到点（0，-1），和点（3y,0）到点（4，-3）的距离和的最小值，这个最小值= ，
∴原式的最小值=2+=2+4．