题目内容
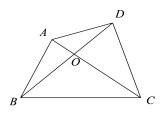
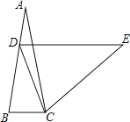
【题目】如图所示,点D是等边△ABC内一点,DA=13,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,求△DEC的周长.

【答案】53.
【解析】
先根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得到AD=AE,CE=BD=19,∠DAE=∠BAC=60°,则可判断△ADE为等边三角形,从而得到DE=AD=13,然后计算△DEC的周长.
∵△ABC 为等边三角形,
∴∠BAC=60°,AB=AC,
∵△ABD 绕点 A 逆时针旋转到△ACE 的位置,
∴AD=AE,CE=BD=19,∠DAE=∠BAC=60°,
∴△ADE 为等边三角形,
∴DE=AD=13,
∴△DEC 的周长=DE+DC+CE=13+21+19=53.

练习册系列答案
相关题目