Question

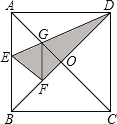
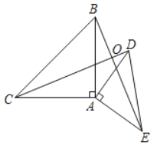
【题目】如图，在Rt△ABC中，∠BAC＝90°，BC＝5，AB＝3，点D是线段BC上一动点，连接AD，以AD为边作△ADE∽△ABC，点N是AC的中点，连接NE，当线段NE最短时，线段CD的长为_____．

Answer 1

【答案】

【解析】

如图，连接EC，作AH⊥BC于H．首先证明EC⊥BC，推出EN⊥EC时，EN的值最小，解直角三角形求出CH，DH即可解决问题；

解：如图，连接EC，作AH⊥BC于H．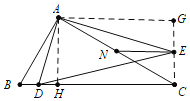

∵△ABC∽△ADE，
∴∠AED=∠ACD，
∴A，D，C，E四点共圆，
∴∠DAE+∠DCE=180°，
∴∠DCE=∠DAE=90°，
∴EC⊥BC，
∴NE⊥EC时，EN的值最小，作AG⊥CE交CE的延长线于G．
在Rt△ABC中，∵BC=5，AB=3，
∴AC=4，
∵△ENC∽△△ACB，
∴，
∴，
∴EC=，
∴AH=CG=，
∵NE∥AG，AN=NC，
∴GE=EC=，
∵∠HAG=∠DAE，
∴∠DAH=∠EAG，

∵∠AHD=∠G=90°，
∴△AHD∽△AGE，
∴，
∴，
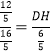∴DH=，
∴CD=DH+CH=．
故答案为．