题目内容
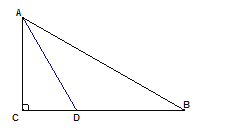
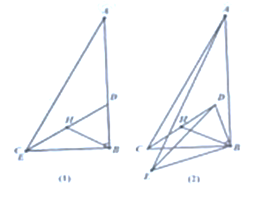
【题目】(1)问题发现:如图(1).在![]() 和
和![]() 中,
中,![]() 绕点
绕点![]() 逆时针旋转.
逆时针旋转.![]() 为
为![]() 边的中点,当点
边的中点,当点![]() 与点
与点![]() 重合时.
重合时.![]() 与
与![]() 的位置关系为 ,
的位置关系为 ,![]() 与
与![]() 的数量关系为 .
的数量关系为 .
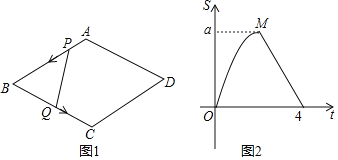
(2)问题证明:在![]() 绕点
绕点![]() 逆时针旋转的过程中,(1)中的结论是否仍然成立,若成立,请仅就图2的情形给出证明,若不成立,请说明理山,
逆时针旋转的过程中,(1)中的结论是否仍然成立,若成立,请仅就图2的情形给出证明,若不成立,请说明理山,
(3)拓展应用:在![]() 绕点
绕点![]() 逆时针旋转旋转的过程中,当
逆时针旋转旋转的过程中,当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
【答案】(1)![]() ;(2)成立,见解析;(3)
;(2)成立,见解析;(3)![]() 或
或![]()
【解析】
(1)如图1,延长BH交AC于点G,根据直角三角形斜边上的中线的性质及已知条件可得∠BDC=∠ABG=60°,进而得到∠A+∠ABG=90°,即可得到BH⊥AE,根据锐角三角函数的定义以及直角三角形斜边上的中线的性质即可得到![]() ;
;
(2)延长![]() 至点
至点![]() ,使
,使![]() ,根据“SAS”证明△DBE≌△PBE,得到
,根据“SAS”证明△DBE≌△PBE,得到![]() ,进而证明
,进而证明![]() ,根据30°直角三角形的性质
,根据30°直角三角形的性质![]() ,从而得到
,从而得到![]() ,再证明
,再证明![]() ,得到
,得到![]() ,根据中位线定理得到
,根据中位线定理得到![]() ,即可得到
,即可得到![]() ,
,![]() ;
;
(3)分两种情况讨论,①①如图3-1中,当DE在BC的下方时,延长AB交DE于点F,根据边角关系以及勾股定理求出AE2,再根据![]() ,即可解答;②如图3-2中,当DE在BC的上方时,同法可得AF,EF的长度,求出求出AE2,再根据
,即可解答;②如图3-2中,当DE在BC的上方时,同法可得AF,EF的长度,求出求出AE2,再根据![]() ,即可解答.
,即可解答.
解:(1)如图1,延长BH交AC于点G,
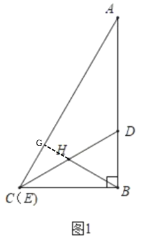
∵点H是Rt△BDC中CD的中点,
∴BH=DH,
∵![]() ,
,
∴∠BDC=∠ABG=60°,
∴∠A+∠ABG=90°,
∴∠AGB=90°,即BH⊥AE,
∵在Rt△ABC中,BC=3,∠A=30°,
∴AE=2BC=6,
在Rt△BDE中,∠DEB=30°,
∴CD=![]() ,
,
∵点H为CD的中点,
∴BH=![]() ,
,
∴![]() ,
,
∴![]()
故答案为:![]()
(2)成立
证明如下:延长![]() 至点
至点![]() ,使
,使![]() ,
,
连接![]() 分别交
分别交![]() 于点
于点![]() ,如图2所示.
,如图2所示.
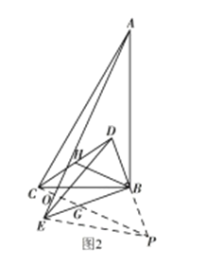
在△DBE与△PBE中,

![]() ,
,
![]()
又![]() ,
, ![]()
![]()
![]()
在![]() 中,
中,![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() 为
为![]() 的中点,
的中点,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
∴(1)中的结论仍然成立,
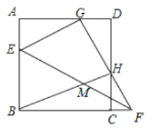
(3)①如图3-1中,当DE在BC的下方时,延长AB交DE于点F,
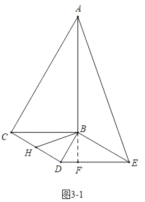
∵DE∥BC,
∴∠ABC=∠BFD=90°,
由题意可知,BC=BE=3,AB=3![]() ,BD=
,BD=![]() ,DE=2
,DE=2![]() ,
,
∴BF=![]() ,
,
EF=![]() ,
,
∴AF=3![]() +
+![]() ,
,
∴AE2=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
②如图3-2中,当DE在BC的上方时,同法可得AF=![]() ,EF=
,EF= ![]() ,
,
∴AE2=![]() ,
,
∴![]()
![]()
综上所述,BH2为![]() 或
或![]() .
.

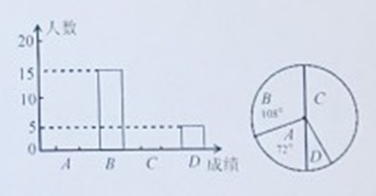
【题目】某校九年级体自模拟测试后,随机抽取了九年级部分学生体有测试成绩进行统计,得到相关的统计图表如下:
成绩/分 |
|
|
|
|
成绩等级 |
|
|
|
|
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的体育测试成绩,补全频数分布直方图
(2)扇形![]() 的圆心角的度数是
的圆心角的度数是
(3)若该校九年级有![]() 名学生,请据此估计该校九年级此次体育测试成绩在
名学生,请据此估计该校九年级此次体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生有多少人?
等级)的学生有多少人?
(4)根据测试中存在的问题,通过一段时间的针对性调练,若![]() 等级学生数可提高
等级学生数可提高![]() 等级学生数可提高
等级学生数可提高![]() ,请估计经过训练后九年级体育测试成绩在
,请估计经过训练后九年级体育测试成绩在![]() 等级以上(含
等级以上(含![]() 等级)的学生可达多少人?
等级)的学生可达多少人?
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
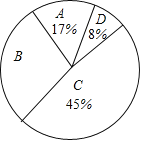
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。