题目内容
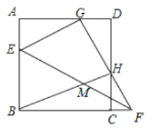
【题目】如图,正方形ABCD中,AB=6,E为AB边上一点,F是BC延长线上一点,将△BEF沿EF翻折,使点B恰好落在AD边上的点G处,FG与CD交于点H,连接BH,与EF交于点M,若BH平分∠CHG,AG=4,则EM=_____.
【答案】![]() .
.
【解析】
由正方形的性质得出AB=BC,∠A=∠ABC=∠BCD=90°,过点B作BP⊥FG于P,连接BG,交EF于N,由翻折的性质得BE=GE,设AE=x,则BE=GE=6-x,在Rt△AEG中,AE2+AG2=GE2,即x2+42=(6-x)2,求出x=![]() ,则BE=GE=
,则BE=GE=![]() ,
,![]() ,由AAS证得△BCH≌△BPH得出∠CBH=∠PBH,BC=BP,推出AB=BP,由HL证得Rt△ABG≌Rt△PBG得出∠ABG=∠PBG,推出∠NBM=∠PBG+∠PBH=
,由AAS证得△BCH≌△BPH得出∠CBH=∠PBH,BC=BP,推出AB=BP,由HL证得Rt△ABG≌Rt△PBG得出∠ABG=∠PBG,推出∠NBM=∠PBG+∠PBH=![]() (∠ABP+∠CBP)=45°,由翻折的性质得出EF垂直平分BG,则BN=NG=
(∠ABP+∠CBP)=45°,由翻折的性质得出EF垂直平分BG,则BN=NG=![]() BG=
BG=![]() ,△BNM是等腰直角三角形,推出MN=BN=
,△BNM是等腰直角三角形,推出MN=BN=![]() ,
,![]() ,即可得出结果.
,即可得出结果.
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=∠BCD=90°,
过点B作BP⊥FG于P,连接BG,交EF于N,如图所示:
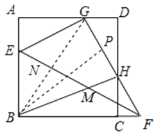
由翻折的性质得:BE=GE,
设AE=x,则BE=GE=6-x,
在Rt△AEG中,AE2+AG2=GE2,
即:x2+42=(6-x)2,
解得:x=![]() ,
,
∴BE=GE=![]() ,
,
![]() ,
,
∵BH平分∠CHG,
∴∠CHB=∠PHB,
在△BCH和△BPH中,
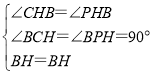 ,
,
∴△BCH≌△BPH(AAS),
∴∠CBH=∠PBH,BC=BP,
∴AB=BP,
在Rt△ABG和Rt△PBG中,
![]() ,
,
∴Rt△ABG≌Rt△PBG(HL),
∴∠ABG=∠PBG,
∴∠NBM=∠PBG+∠PBH=![]() (∠ABP+∠CBP)=
(∠ABP+∠CBP)=![]() ×90°=45°,
×90°=45°,
由翻折的性质得:EF垂直平分BG,
∴BN=NG=![]() BG=
BG=![]() ,△BNM是等腰直角三角形,
,△BNM是等腰直角三角形,
∴MN=BN=![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() .
.