Question

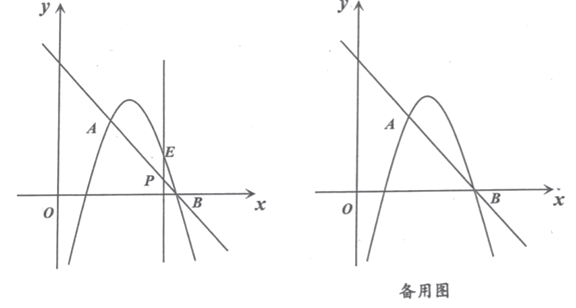
【题目】在平面直角坐标系xOy中，抛物线y＝ax2+bx+c的开口向上，与x轴相交于A、B两点（点A在点B的右侧），点A的坐标为（m，0），且AB＝4．

（1）填空：点B的坐标为　 　（用含m的代数式表示）；

（2）把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P，△ABP的面积为8：

①求抛物线的解析式（用含m的代数式表示）；

②当0≤x≤1，抛物线上的点到x轴距离的最大值为时，求m的值．

Answer 1

【答案】（1）（m﹣4，0）；（2）①y＝（x﹣m）（x﹣m+4）；②m的值为：2+2或3﹣2或2≤m≤3．

【解析】

（1）A的坐标为（m，0），AB=4，则点B坐标为（m-4，0）；

（2）①S△ABP= AByP=2yP=8，即：yP=4，求出点P的坐标为（4+m，4），即可求解；

②抛物线对称轴为x=m-2．分x=m-2≥1、0≤x=m-2≤1、x=m-2≤0三种情况，讨论求解.

解：（1）A的坐标为（m，0），AB＝4，则点B坐标为（m﹣4，0），故答案为（m﹣4，0）；

（2）①S△ABP＝AByP＝2yP＝8，∴yP＝4，

把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P，此时，直线AP表达式中的k值为1，

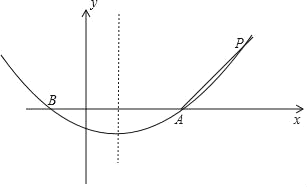
设：直线AP的表达式为：y＝x+b，

把点A坐标代入上式得：m+b＝0，即：b＝﹣m，

则直线AP的表达式为：y＝x﹣m，

则点P的坐标为（4+m，4），

则抛物线的表达式为：y＝a（x﹣m）（x﹣m+4），

把点P坐标代入上式得：a（4+m﹣m）（4+m﹣m+4）＝4，

解得：a＝，

则抛物线表达式为：y＝（x﹣m）（x﹣m+4），

②抛物线的对称轴为：x＝m﹣2，

当x＝m﹣2≥1（即：m≥3）时，x＝0时，抛物线上的点到x轴距离为最大值，

即：（0﹣m）（0﹣m+4）＝，解得：m＝2或2±2，

∵m≥3，故：m＝2+2；

当0≤x＝m﹣2≤1（即：2≤m≤3）时，在顶点处，抛物线上的点到x轴距离为最大值，

即：﹣（m﹣2﹣m）（m﹣2﹣m+4）＝，符合条件，

故：2≤m≤3；

当x＝m﹣2≤0（即：m≤2）时，x＝1时，抛物线上的点到x轴距离为最大值，

即：（1﹣m）（1﹣m+4）＝，解得：m＝3或3±2，

∵m≤2，故：m＝3﹣2；

综上所述，m的值为：2+2或3﹣2或2≤m≤3．