��Ŀ����
����Ŀ����ͼ����¥AN������һ����AB��Сӱ������D�������������A������Ϊ30�㣬�����������ߵ��½�E����Ȼ�����¥�����������10������C������������ĵײ�B������Ϊ45�㣬��ʱСӱ���¥��N��20�ף���֪����DE=20�ף�ɽ�µ��¶�i=1��![]() ����tan��DEM=1��
����tan��DEM=1��![]() ������D��M��E��C��N��B��A��ͬһƽ���ڣ�E��C��N��ͬһ��ֱ���ϣ��������ij��ȣ������ȷ��1�ף����ο����ݣ�
������D��M��E��C��N��B��A��ͬһƽ���ڣ�E��C��N��ͬһ��ֱ���ϣ��������ij��ȣ������ȷ��1�ף����ο����ݣ�![]() ��1.73��
��1.73��![]() ��1.41��
��1.41��
���𰸡��⣺����D��DH��AN��H������E��FE����DH��F��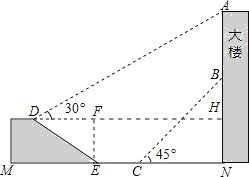
������DE=20�ף�ɽ�µ��¶�i=1��![]() ��
��
��EF=10�ף�DF=![]() �ף�
�ף�
��DH=DF+EC+CN=��![]() +30���ף���ADH=30�㣬
+30���ף���ADH=30�㣬
��AH=![]() ��DH=��10+
��DH=��10+![]() ���ף�
���ף�
��AN=AH+EF=��20+![]() ���ף�
���ף�
�ߡ�BCN=45�㣬
��CN=BN=20�ף�
��AB=AN��BN=![]() ��17�ף�
��17�ף�
�������ij�����17�ף�
������������D��DH��AN��H������E��FE����DH��F���������DF�ij������������DH�ij�����ֱ��������ADH�У������AH�ij������������AN�ij�����ֱ��������CNB�п����BN�ij�������AB=AH��BN���㼴�ɣ�

��ϰ��ϵ�д�
�����Ŀ





