题目内容
【题目】如图，在ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将ABCD沿EF折叠，得到四边形EFGH，点A的对应点为点H，点D的对应点为点G．
（1）当点H与点C重合时．
①填空：点E到CD的距离是___；
②求证：△BCE≌△GCF；
③求△CEF的面积；
（2）当点H落在射线BC上，且CH=1时，直线EH与直线CD交于点M，请直接写出△MEF的面积．
【答案】
（1）
解：如图1，
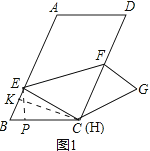
①作CK⊥AB于K，
∵∠B=60°，
∴CK=BCsin60°=4×
=2
，
∵C到AB的距离和E到CD的距离都是平行线AB、CD间的距离，
∴点E到CD的距离是2，
故答案为2；
②∵四边形ABCD是平行四边形，
∴AD=BC，∠D=∠B，∠A=∠BCD，
由折叠可知，AD=CG，∠D=∠G，∠A=∠ECG，
∴BC=GC，∠B=∠G，∠BCD=∠ECG，
∴∠BCE=∠GCF，
在△BCE和△GCF中，
，
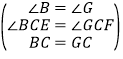∴△BCE≌△GCF（ASA）；
③过E点作EP⊥BC于P，
∵∠B=60°，∠EPB=90°，
∴∠BEP=30°，
∴BE=2BP，
设BP=m，则BE=2m，
∴EP=BEsin60°=2m×=m，
由折叠可知，AE=CE，
∵AB=6，
∴AE=CE=6﹣2m，
∵BC=4，
∴PC=4﹣m，
在Rt△ECP中，由勾股定理得（4﹣m）2+（m）2=（6﹣2m）2，解得m=
，
∴EC=6﹣2m=6﹣2×=
，
∵△BCE≌△GCF，
∴CF=EC=，
∴S△CEF=
××2=
；
（2）
解：①当H在BC的延长线上，且位于C点的右侧时时，如图2，过E点作EQ⊥BC于Q，
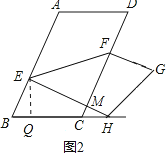
∵∠B=60°，∠EQB=90°，
∴∠BEQ=30°，
∴BE=2BQ，
设BQ=n，则BE=2n，
∴QE=BEsin60°=2n×=n，
由折叠可知，AE=HE，
∵AB=6，
∴AE=HE=6﹣2n，
∵BC=4，CH=1，
∴BH=5，
∴QH=5﹣n，
在Rt△EHQ中，由勾股定理得（5﹣n）2+（n）2=（6﹣2n）2，解得n=
，
∴AE=HE=6﹣2n=
，
∵AB∥CD，
∴△CMH∽△BEH，
∴
=
，即
=
，
∴MH=
，
∴EM=﹣=
∴S△EMF=××2=
．
②如图3，当H在线段BC上时，过E点作EQ⊥BC于Q，
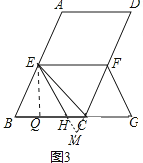
∵∠B=60°，∠EQB=90°，
∴∠BEQ=30°，
∴BE=2BQ，
设BQ=n，则BE=2n，
∴QE=BEsin60°=2n×=n，
由折叠可知，AE=HE，
∵AB=6，
∴AE=HE=6﹣2n，
∵BC=4，CH=1，
∴BH=3
∴QH=3﹣n
在Rt△EHQ中，由勾股定理得（3﹣n）2+（n）2=（6﹣2n）2，解得n=
∴BE=2n=3，AE=HE=6﹣2n=3，
∴BE=BH，
∴∠B=60°，
∴△BHE是等边三角形，
∴∠BEH=60°，
∵∠AEF=∠HEF，
∴∠FEH=∠AEF=60°，
∴EF∥BC，
∴DF=CF=3，
∵AB∥CD，
∴△CMH∽△BEH，
∴
=，即
=
，
∴CM=1
∴EM=CF+CM=4
∴S△EMF=×4×2=4．
综上，△MEF的面积为或4．
【解析】（1）①解直角三角形即可；
②根据平行四边形的性质和折叠的性质得出∠B=∠G，∠BCE=∠GCF，BC=GC，然后根据AAS即可证明；③过E点作EP⊥BC于P，设BP=m，则BE=2m，通过解直角三角形求得EP=m，然后根据折叠的性质和勾股定理求得EC，进而根据三角形的面积就可求得；
（2）过E点作EQ⊥BC于Q，通过解直角三角形求得EP=n，根据折叠的性质和勾股定理求得EH，然后根据三角形相似对应边成比例求得MH，从而求得CM，然后根据三角形面积公式即可求得．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．
