Question

【题目】某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售，已知每天包装大黄米的质量是包装江米质量的倍，且每天包装大黄米和江米的质量之和为45千克．
（1）求平均每天包装大黄米和江米的质量各是多少千克？
（2）为迎接今年6月20日的“端午节”，该超市决定在前20天增加每天包装大黄米和江米的质量，二者的包装质量与天数的变化情况如图所示，节日后又恢复到原来每天的包装质量．分别求出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式，并写出自变量的取值范围．

（3）假设该超市每天都会将当天包装后的大黄米和江米全部售出，已知大黄米成本价为每千克7.9元，江米成本每千克9.5元，二者包装费用平均每千克均为0.5元，大黄米售价为每千克10元，江米售价为每千克12元，那么在这20天中有哪几天销售大黄米和江米的利润之和大于120元？[总利润=售价额﹣成本﹣包装费用]．

Answer 1

【答案】
（1）

解：设平均每天包装大黄米和江米的质量分别为a千克和b千克，则 ，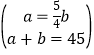

解得；

答：平均每天包装大黄米和江米的质量分别为25千克和20千克．

（2）

解：观察图象，可设平均每天包装大黄米的质量与天数的关系式为y=k1x+b1，平均每天包装江米的质量与天数的关系式为y=k2x+b2．

①当0≤x≤15 时，由y=k1x+b1 的图象过点（0，25），（15，40）．

则可列方程组为，解得，

∴y1=x+25；

由y=k2x+b2 的图象过点（0，20），（15，38）．

则可列方程组为，解得，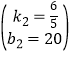

∴；

②当15＜x≤20时，

由y=k1x+b1 的图象过点（15，40），（20，25）．

则可列方程组为，解得，

∴y1=﹣3x+85；

由y=k2x+b2 的图象过点（15，38），（20，20）．

则可列方程组为，解得，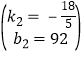

∴y2=，

∴，．

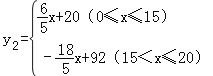（3）

解：设第x天销售的总利润为W元，

①当0≤x≤15 时，W=（10﹣7.9﹣0.5）y1+（12﹣9.5﹣0.5）y2=1.6y1+2y2=1.6（x+25）+2（1.2x+20）=4x+80．

由题意4x+80＞120，∴x＞10，

∴x的取值范围为10＜x≤15，

由题意知 x=11，12，13，14，15；

②当15＜x≤20 时，W=（10﹣7.9﹣0.5）y1+（12﹣9.5﹣0.5）y2=1.6y1+2y2=1.6（﹣3x+85）+2（）=﹣12x+30．

由题意得：﹣12x+320＞120，

∴x＜，

∴x的取值范围为15．

由题意知x=16．

答：由①、②可知在第11，12，13，14，15，16天中销售大黄米和江米的总利润大于120元．

【解析】（1）设平均每天包装大黄米和江米的质量分别为a千克和b千克，然后列方程组求解即可；
（2）设出函数的解析式，利用待定系数法求解即可；
（3）根据销售大黄米和江米的利润之和大于120元列不等式求解即可．