题目内容
【题目】阅读下面材料：
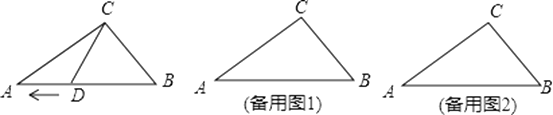
小明遇到这样一个问题：如图1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系．
小明发现，利用轴对称做一个变化，在BC上截取CA′=CA，连接DA′，得到一对全等的三角形，从而将问题解决（如图2）．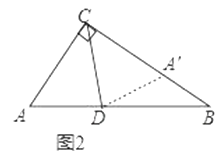
请回答：
（1）在图2中，小明得到的全等三角形是△≌△；
（2）求BC和AC、AD之间的数量关系是
（3）参考小明思考问题的方法，解决问题：
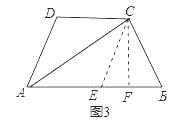
如图3，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9．求AB的长．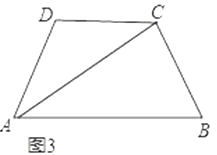
【答案】
（1）ADC,A′DC
（2）BC=AC+AD
（3）解：如图，在AB上截取AE=AD，连接CE，如图3所示：
∵AC平分∠BAD，
∴∠DAC=∠EAC．
在△AEC和△ADC中，
，
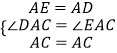∴△ADC≌△AEC（SAS），
∴AE=AD=9，CE=CD=10=BC，
过点C作CF⊥AB于点F，
∴EF=BF，
设EF=BF=x．
在Rt△CFB中，∠CFB=90°，由勾股定理得CF2=CB2-BF2=102-x2，
在Rt△CFA中，∠CFA=90°，由勾股定理得CF2=AC2-AF2=172-（9+x）2．
∴102-x2=172-（9+x）2，
解得：x=6，
∴AB=AE+EF+FB=9+6+6=21，
∴AB的长为21．
【解析】（1）由SAS容易证出△ADC≌△A′DC;
(2)由△ADC≌△A′DC;得出DA′=DA,∠DA′C=∠A=60
,再证出BA′=DA′,得出BA′=AD，即可得出结论；
解决问题：如图，在AB上截取AE=AD，连接CE，先证明△ADC≌△AEC，得出AE=AD=9，CE=CD=10=BC，过点C作CF⊥AB于点F，设EF=BF=x．在Rt△CFB中和Rt△CFA中根据勾股定理求出x，即可得出结论。
