Question

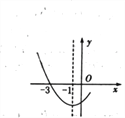
【题目】已知：抛物线C1：y=x2－2a x+2a+2 顶点P在另一个函数图象C2上，

（1）求证：抛物线C1必过定点A（1，3）；并用含的a式子表示顶点P的坐标；

（2）当抛物线C1的顶点P达到最高位置时，求抛物线C1解析式；并判断是否存在实数m、n，当m≤x≤n时恰有3m≤y≤3n，若存在，求出求m、n的值；若不存在，说明理由；

（3）抛物线C1和图象C2分别与y轴交于B、C点，当△ABC为等腰三角形，求a的值．

Answer 1

【答案】（1）顶点P(a，－a 2+2a+2) （2）m=1， n=4 （3）,或，或a =1，a =0（B与C重合，舍去）

【解析】试题分析：（1）根据待定系数法，直接把A点的坐标x=1代入即可证明抛物线C1必过定点A，然后根据配方法求出顶点P的坐标；

（2）先根据配方法求出yP=－(a-1) 2+3≤3，得到P的最高点的坐标，求得C1解析式，然后根据二次函数的最值以及二次函数的增减性可求出m、n的值；

（3）分别求出两函数和y轴的交点，然后结合等腰三角形和勾股定理分类讨论即可求出a的值.

试题解析：（1）∵当时，

∴ 抛物线C1必过定点A（1，3）

∵抛物线C1：y=x2－2a x+2a+2=（x－a）2－a 2+2a+2

∴顶点P(a，－a 2+2a+2)

（2）∵yP=－a 2+2a+2=－(a-1) 2+3≤3

∴当时，P达到最高位置（1，3）

此时抛物线C1解析式为y=x2－2 x+4

∴ y=x2－2 x+4=（x－1）2+3 ≥3

∵当m≤x≤n时恰有3m≤y≤3n

∴3≤3m≤y≤3n

∴1≤m≤n

∴当1≤m≤x≤n ，y随x的增大面增大

∴当x= m 时， y= 3m，当x= n 时，y= 3 n

∴解得

∵ 1≤m≤n

∴m=1， n=4

（3）∵抛物线C1：y=x2－2a x+2a+2与y轴交于B点

∴B（0，2a+2）

∵函数yP=－x 2+2x+2图象C2与y轴交于C点

∴C（0，2）

∵A（1，3）

∴由勾股定理得AC=，BC = ，AB2=( a -1) 2+1

∵△ABC为等腰三角形

∴①AC=BC ②BC 2= AB2 ③AC 2= AB2

∴= 或 4 a 2 =(2 a -1) 2+1 或2= (2 a -1) 2+1

∴,或，或a =1，a =0（B与C重合，舍去）