题目内容
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(-3,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为 . 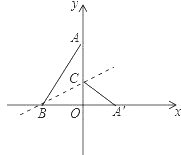
【答案】(0,![]() )
)
【解析】∵A(0,4),B(-3,0),
∴OA=4,OB=3,
在Rt△OAB中,AB= ![]() ,
,
∵△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,
∴BA′=BA=5,CA′=CA,
∴OA′=BA′-OB=5-3=2,
设OC=t,则CA=CA′=OA-OC=4-t,
在Rt△OA′C中,由勾股定理得:OC2+OA′2=CA′2,
即t2+22=(4-t)2,
解得:t= ![]() ,
,
∴C点坐标为(0, ![]() ).
).
【考点精析】通过灵活运用勾股定理的概念和翻折变换(折叠问题),掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
相关题目
【题目】商店某天销售了14件衬衫,其领口尺寸统计如表:
领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
件数 | 1 | 5 | 3 | 3 | 2 |
则这14件衬衫领口尺寸的众数与中位数分别是( )
A.39cm、39cm
B.39cm、39.5cm
C.39cm、40cm
D.40cm、40cm