题目内容
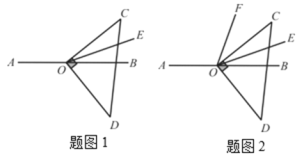
【题目】已知点O为直线AB上一点,将一个直角三角板COD的直角顶点放在点O处,并使OC边始终在直线AB的上方,OE平分∠BOC.

(1)如图1,若∠DOE=70°,则∠AOC =___________°;
(2)如图1,若∠DOE=α,求∠AOC的度数;(用含α的式子表示)
(3)如图2,在(2)的条件下,若在∠AOC的内部有一条射线OF,满足∠BOE =![]() (∠AOF-∠DOE),试确定∠AOF与∠DOE之间的数量关系,并说明理由.
(∠AOF-∠DOE),试确定∠AOF与∠DOE之间的数量关系,并说明理由.
【答案】(1)140°;(2)![]() ;(3)∠AOF+∠DOE=180° (或 ∠AOF与∠DOE互补 ),理由见解析
;(3)∠AOF+∠DOE=180° (或 ∠AOF与∠DOE互补 ),理由见解析
【解析】
(1)由角平分线的性质及同角的余角相等,可得答案;
(2)类比(1),由角平分线的性质及同角的余角相等,可得出∠AOC的度数;
(3)由∠BOE=![]() (∠AOF-∠DOE),得出180°-∠AOC=∠AOF-∠DOE,再根据∠DOE =
(∠AOF-∠DOE),得出180°-∠AOC=∠AOF-∠DOE,再根据∠DOE =![]() ,∠AOC =2
,∠AOC =2![]() 解答即可.
解答即可.
(1)解: ∵∠DOC=90°, ∠DOE=70°,
∴∠COE=20°,
∵OE平分∠BOC,
∴∠COE=∠BOE=20°,
∴∠BOC=40°,
∵∠AOC+∠BOC=180°,
∴∠AOC=140°
(2)解:∵∠DOE =![]()
![]() ∠COE=90°
∠COE=90°![]()
∵OE平分∠BOC
![]() ∠BOC=2∠COE=180°
∠BOC=2∠COE=180°![]()
![]() ∠AOC=180°-∠BOC=180°-(180°
∠AOC=180°-∠BOC=180°-(180°![]() )=
)=![]()
(3)∠AOF+∠DOE=180° (或 ∠AOF与∠DOE互补 )
理由如下:
∵∠BOE=![]() (∠AOF-∠DOE)
(∠AOF-∠DOE)
![]() 2∠BOE= ∠AOF-∠DOE
2∠BOE= ∠AOF-∠DOE
![]() ∠BOC=∠AOF-∠DOE
∠BOC=∠AOF-∠DOE
![]() 180°-∠AOC=∠AOF-∠DOE
180°-∠AOC=∠AOF-∠DOE
∵∠DOE =![]() ,∠AOC =2
,∠AOC =2![]()
![]() ∠AOC=2∠DOE
∠AOC=2∠DOE
![]() 180°-2∠DOE=∠AOF-∠DOE
180°-2∠DOE=∠AOF-∠DOE
![]() ∠AOF+∠DOE=180°,即∠AOF与∠DOE互补.
∠AOF+∠DOE=180°,即∠AOF与∠DOE互补.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表)。
月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |

设一个月内使用移动电话主叫的时间为![]() 分(
分(![]() 为正整数),请根据表中提供的信息回答下列问题:
为正整数),请根据表中提供的信息回答下列问题:
(1)用含有![]() 的式子填写下表:
的式子填写下表:
| 150< |
|
| |
方式一计费/元 | 58 |
| 108 |
|
方式二计费/元 | 88 | 88 | 88 |
|
(Ⅰ)当![]() 为何值时,两种计费方式的费用相等?
为何值时,两种计费方式的费用相等?
(Ⅱ)请根据(Ⅰ)和(Ⅱ)的计算及生活经验,直接写出不同时间段,选用哪种计费方式省钱.