题目内容
【题目】如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
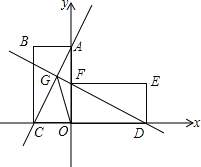
(1)求直线DF的解析式;
(2)求证:GO平分∠CGD;
(3)在角平分线GO上找一点M,使以点G、M、D为顶点的三角形是等腰直角三角形,求出M点坐标.
【答案】(1)y=﹣![]() x+1(2)见解析(3)M点的坐标为(
x+1(2)见解析(3)M点的坐标为(![]() ,﹣
,﹣![]() )和(
)和(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)根据直线的解析式找出点A、C的坐标,再由旋转的特性找出点D、F的坐标,结合点D、F的坐标利用待定系数法即可求出直线DF的解析式;
(2)过点O作OP⊥AC于点P,作OQ⊥DG于点Q,利用全等直角三角形的判定定理HL证出Rt△OAC≌Rt△ODF和Rt△OPG≌Rt△OQG,由此即可得出∠PGO=∠QGO,从而证出GO平分∠CGD;
(3)根据旋转的性质可得出AC⊥DF,结合(2)的结论即可得出∠OGD=45°,联立直线AC、DF的解析式成方程组,解方程组可得出点G的坐标,根据等腰直角三角形的性质可分两种情况寻找点M的位置,再通过勾股定理解方程等即可得出结论.
解:(1)∵直线y=2x+2交y轴于A点,交x轴于C点,
∴A点的坐标是(0,2),C点的坐标是(﹣1,0),
∵将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,
∴F点的坐标是(0,1),D点的坐标是(2,0),
设直线DF的解析式是y=kx+1,
∴2k+1=0,
解得k=﹣![]() ,
,
∴直线DF的解析式是:y=﹣![]() x+1.
x+1.
(2)过点O作OP⊥AC于点P,作OQ⊥DG于点Q,如图1所示.
在Rt△OAC和Rt△ODF中,![]() ,
,
∴Rt△OAC≌Rt△ODF(HL),
又∵OP⊥AC,OQ⊥DG,
∴OP=OQ,
在Rt△OPG和Rt△OQG中,![]() ,
,
∴Rt△OPG≌Rt△OQG(HL),
∴∠PGO=∠QGO,
∴OG平分∠CGD.
(3)∵矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,
∴对角线AC⊥DF,
∵GO平分∠CGD,
∴∠OGD=45°.
解 得:
得: ,
,
即点G(﹣![]() ,
,![]() ),
),
∴直线GO为y=﹣3x.
∵D(2,0),
∴GD=![]() =
=![]() ,GO=
,GO=![]() =
=![]() .
.
以点G、M、D为顶点的三角形是等腰直角三角形分两种情况:
①过D作DM1⊥GO于点M1,则△GM1D是以GD为斜边的等腰直角三角形,过M1作M1H⊥OD于点H,如图2所示.
∵GD=![]() ,
,
∴GM1=DM1=![]() ×
×![]() =
=![]() .
.
∵GO=![]() ,
,
∴OM1=GM1﹣GO=![]() ﹣
﹣![]() =
=![]() .
.
设点M1(x,﹣3x),在Rt△OM1H中有![]() ,
,
即x2+(﹣3x)2=![]() ,解得:x=
,解得:x=![]() 或x=﹣
或x=﹣![]() (舍去).
(舍去).
∴点M1(![]() ,﹣
,﹣![]() );
);
②过D作DM2⊥GD交GO于M2,则△GM2D是以GD为直角边的等腰直角三角形,过M2作M2I⊥OD于点I,如图3所示.
∵GD=![]() ,
,
∴GM2=![]() ×
×![]() =
=![]() ,
,
∵GO=![]() ,
,
∴OM2=GM2﹣GO=![]() ﹣
﹣![]() =
=![]() .
.
设M2(a,﹣3a),在Rt△OM2I中有![]() ,
,
即a2+(﹣3a)2=![]() ,解得:a=
,解得:a=![]() 或a=﹣
或a=﹣![]() (舍去),
(舍去),
∴点M2(![]() ,﹣
,﹣![]() ).
).
综上可得:使以点G、M、D为顶点的三角形是等腰直角三角形的M点的坐标为(![]() ,﹣
,﹣![]() )和(
)和(![]() ,﹣
,﹣![]() ).
).




 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案