题目内容
如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B、C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E.设BP=x,△PCE面积为y,则y与x的函数关系式是

A.y=2x+1 B. C.
C.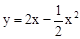 D.y=2x
D.y=2x

A.y=2x+1 B.
 C.
C.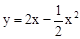 D.y=2x
D.y=2xC
试题分析:如图,过点E作EH⊥BC于点H,

∵四边形ABCD是正方形,∴∠DCH=90°。
∵CE平分∠DCH,∴∠ECH=
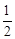 ∠DCH=45°。
∠DCH=45°。∵∠H=90°,∴∠ECH=∠CEH=45°。∴EH=CH。
∵四边形ABCD是正方形,AP⊥EP,∴∠B=∠H=∠APE=90°。
∴∠BAP+∠APB=90°,∠APB+∠EPH=90°。∴∠BAP=∠EPH。
∵∠B=∠H=90°,∴△BAP∽△HPE。∴
 ,即
,即 。∴EH=x。
。∴EH=x。∴y=
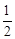 ×CP×EH=
×CP×EH=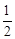 (4﹣x)•x=2x﹣
(4﹣x)•x=2x﹣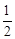 x2。
x2。故选C。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目






 ,则点D的坐标为 .
,则点D的坐标为 . 
 ,
, ,
, ,
, 分别是
分别是 ,
, ,
, 的中点,设
的中点,设 ,
, ,则
,则 是( ).
是( ). ;
; ;
; ;
;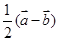 .
.