题目内容
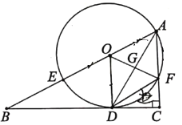
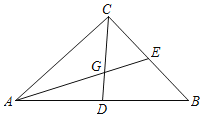
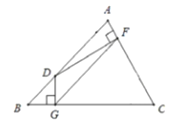
【题目】已知:△ABC中,∠B=45°,∠C=60°,BC=4,D、F分别为AB、AC边上的一个动点,过D分别作DF⊥AC于F,DG⊥BC于G,那么FG的最小值为()
A.2B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接CD,利用90°圆周角所对的弦是直径可得点D,G,C,F四点共圆,且CD是圆的直径,当FG⊥CD时,FG最小,利用垂径定理可得CD平分∠ACB,然后设DG=BG=x,则CG=4-x,然后利用三角函数求得x的值,从而求得GF的长度.
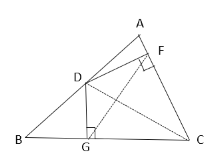
解:如图,连接CD.
由题意可知:∠DGC=∠DFC=90°
∴点D,G,C,F四点共圆,且CD是圆的直径,
当FG⊥CD时,FG最小,
∵FG⊥CD
∴直径CD垂直平分FG
又∵∠ACB=60°
△ABC为等边三角形
∴GF=CG
∵∠B=45°,∠DGC =90°
∴设DG=BG=x,则CG=4-x,
在Rt△DCG中,∠GCD=30°
∴![]() ,即
,即![]()
解得:![]()
∴GF=GC=4-x=![]()
故选:C.

练习册系列答案
相关题目
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的