题目内容
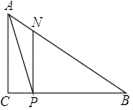
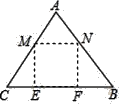
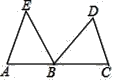
【题目】如图,在△ABE中,C为边AB延长线上一点,BC=AE,点D在∠EBC内部,且∠EBD=∠A=∠DCB.
(1)求证:△ABE≌△CDB.
(2)连结DE,若∠CDB=60°,∠AEB=50°,求∠BDE的度数.
【答案】(1)见解析;(2)55o
【解析】
(1)利用∠ABE+∠EBD+∠DBC=180,∠A+∠AEB+∠EBA=180°,的关系, 求出∠BDC=∠EBA,再利用AAS证明△ABE≌△CDB.
( 2 )利用△ABE≌△CDB,得出BE=DB,即∠BED=∠BDE,再利用∠ABE+∠EBD+∠BDC=180°之间的关系求出∠EBD的度数.
证明:(1)∵∠ABE+∠EBD+∠DBC=180°,∠A+∠AEB+∠EBA=180°,
∵∠EBD=∠A=∠DCB,
∴∠EBA=∠DBC,
在△ABE与△CDB中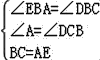 ,
,
∴△ABE≌△CDB(AAS),
(2)∵△ABE≌△CDB,
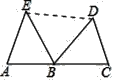
∴BE=DB,∠AEB=∠DBC,
∵∠CDB=60°,∠AEB=50°,
∴∠DBC=50°,
∴∠C=180°﹣60°﹣50°=70°,
∴∠EBD=∠DCB=70°,
∴∠BDE=![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目