题目内容
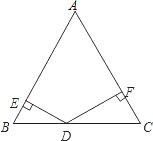
如图,已知边长为2的正三角形ABC沿着直线l滚动.设△ABC滚动240°时,C点的位置为C′,△ABC滚动480°时,A点的位置为A′.请你利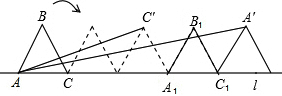 用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )
用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )
 用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )
用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )| A.30° | B.90° | C.60° | D.45° |
∵△ABC滚动240°时,C点的位置为C′,△ABC滚动480°时,A点的位置为A′,
过B作BD⊥AC于D,由等边三角形性质得:AD=1=CD,
由因为正三角形ABC的高BD=
=
,
tan∠CAC′=
=
,
tan∠CAA′=
=
,
∵由公式tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ)得:
tan(∠CAC′+∠CAA′)=(tan∠CAC′+tan∠CAA′)÷(1-tan∠CAC′•tan∠CAA′)=(
+
)÷(1-
×
)=
.
∴∠CAC’+∠CAA’=30°,
故选A.

过B作BD⊥AC于D,由等边三角形性质得:AD=1=CD,
由因为正三角形ABC的高BD=
| 22-12 |
| 3 |
tan∠CAC′=
| ||
| 2+2+1 |
| ||
| 5 |
tan∠CAA′=
| ||
| 4×2+1 |
| ||
| 9 |
∵由公式tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ)得:
tan(∠CAC′+∠CAA′)=(tan∠CAC′+tan∠CAA′)÷(1-tan∠CAC′•tan∠CAA′)=(
| ||
| 5 |
| ||
| 9 |
| ||
| 5 |
| ||
| 9 |
| ||
| 3 |
∴∠CAC’+∠CAA’=30°,
故选A.

练习册系列答案
相关题目