题目内容
【题目】已知菱形ABCD的边长为1，∠DAB=60°，E为AD上的动点，F在CD上，且AE＋CF=1，
设△BEF的面积为y，AE=x，当点E运动时，能正确描述y与x关系的图像是（ ）
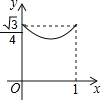
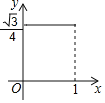
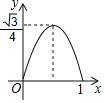
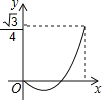
A. B. C. D.
【答案】A
【解析】证明△BEF是等边三角形，求出△BEF的面积y与x的关系式，即可得出答案.
解：连接BD，如图所示：
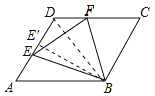
∵菱形ABCD的边长为1，∠DABA=60°，
∴△ABD和△BCD都为正三角形，
∴∠BDE=∠BCF=60°，BD=BC，
∵AE+DE=AD=1，二AE+CF=1，
∴DE=CF，
在△BDE和△BCF中，
DE=CF，∠BDE=∠C，BD=BC，
∴△BDE≌△BCF（SAS）；
∴∠DBE=∠CBF，BE=BF，
∵∠DBC=∠DBF+∠CBF=60°，
∴△AEF为正三角形；
∴BE=EF，△BEF的面积y=
BE2，
作BE/⊥AD于E/，则AE/=
AD=，BE/=
，
∵AE=x，
∴EE/=-x，
∴BE2=(-x)2+（）2，
∴y=（x-）2+
（0≤x≤1）.
故选A.
“点睛”此题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质、动点问题的函数图象、三角形的面积问题. 求出y与x 的函数关系式是解决问题的关键.
练习册系列答案
相关题目
