题目内容
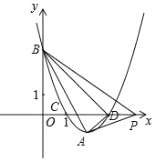
【题目】已知顶点为A(2,﹣1)的抛物线与y轴交于点B,与x轴交于C、D两点,点C坐标(1,0);
(1)求这条抛物线的表达式;
(2)连接AB、BD、DA,求![]() 的大小;
的大小;
(3)点P在x轴正半轴上位于点D的右侧,如果∠APB=45°,求点P的坐标.
【答案】(1)y=x2﹣4x+3 (2)![]() (3)点P(3+
(3)点P(3+![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x-2)2-1,将点C的坐标代入可求得a的值,从而可得到抛物线的解析式;
(2)先求得点B、C、D的坐标,由点A、B、D的坐标可得到∠BDO=∠ADO=45°,从而可证明△ABD为直角三角形,然后依据两点间的距离公式可求得AB和BD的长,最后依据余弦定理的定义求解即可;
(3)先证明△ADP∽△PDB,依据相似三角形的性质可得到DP2=BD×AD,从而可求得DP的长,故此可得到点P的坐标.
解:(1)∵顶点为A(2,﹣1)的抛物线经过点C(1,0),
∴可以假设抛物线的解析式为y=a(x﹣2)2﹣1,
把(1,0)代入可得a=1,
∴抛物线的解析式为y=x2﹣4x+3.
(2)令y=0,x2﹣4x+3=0,解得x=1或3,
∴C(1,0),D(3,0),令x=0,y=3,
∴B(0,3)∵OB=OD=3,∴∠BDO=45°,
∵A(2,﹣1),D(3,0),
∴∠ADO=45°,∴∠BDA=90°,∴![]() ·
·
(3)∵∠BDO=∠DPB+∠DBP=45°,∠APB=∠DPB+∠DPA=45°,∴∠DBP=∠APD,
∵∠PDB=∠ADP=135°,∴△PDB∽△ADP,∴PD2=BDAD=3![]() ×
×![]() =6,
=6,
∴PD=![]() ,∴OP=3+
,∴OP=3+![]() ,∴点P(3+
,∴点P(3+![]() ,0).
,0).
“点睛”本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、锐角三角函数的定义、学生三角形的性质和判断,证得△ABD为直角三角形是解答问题(2)的关键;证得△ADP∽△PDB是解答问题(3)的关键.