Question

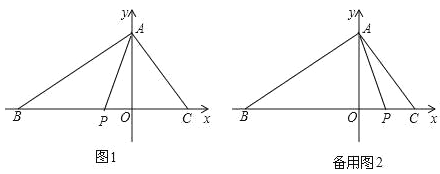
【题目】如图，在平面直角坐标系中，O为坐标原点．△ABC的边BC在x轴上，A、C两点的坐标分别为A（0，m）、C（n，0），B（-5，0），且，点P从B出发，以每秒2个单位的速度沿射线BO匀速运动，设点P运动时间为t秒．

（1）求A、C两点的坐标；

（2）连接PA，用含t的代数式表示△POA的面积；

（3）当P在线段BO上运动时，在y轴上是否存在点Q，使△POQ与△AOC全等？若存在，请求出t的值并直接写出Q点坐标；若不存在，请说明理由．

Answer 1

【答案】（1）A的坐标是（0，4），C的坐标是（3，0）；（2）当0≤t＜时，s=10-4t；当t=时,s=0；当t＞时，

【解析】

试题分析：（1）根据偶次方和算术平方根的非负性得出n-3=0，3m-12=0，求出即可；

（2）分为三种情况：当0≤t＜时，P在线段OB上，②当t=时，P和O重合，③当t＞时，P在射线OC上，求出OP和OA，根据三角形的面积公式求出即可；

（3）分为四种情况：①当BP=1，OQ=3时，②当BP=2，OQ=4时，③④利用图形的对称性直接写出其余的点的坐标即可．

试题解析：（1）∵，

∴n-3=0，3m-12=0，

n=3，m=4，

∴A的坐标是（0，4），C的坐标是（3，0）；

（2）∵B（-5，0），

∴OB=5，

①当0≤t＜时，P在线段OB上，如图1，

∵OP=5-2t，OA=4，

∴△POA的面积S=×OP×AP=×（5-2t）×4=10-4t；

②当t=时，P和O重合，此时△APO不存在，即S=0；

③当t＞时，P在射线OC上，如备用图2，

∵OP=2t-5，OA=4，

∴△POA的面积S=×OP×AP=×（2t-5）×4=4t-10；

（3）当P在线段BO上运动时，在y轴上存在点Q，使△POQ与△AOC全等，

∵P在线段BO上运动，

∴t≤5÷2=2．5，

①当BP=1，OQ=3时，△POQ和△AOC全等，

此时t=，Q的坐标是（0，3）；

②当BP=2，OQ=4时，△POQ和△AOC全等，

此时t==1，Q的坐标是（0，4）；

③④由对称性可知Q为（0，-3）、（0，-4）

综上所述，t=或1时，Q的坐标是（0，3）或（0，4）或（0，-3）或（0，-4）．