题目内容
【题目】如图，在长方形
中，
为平面直角坐标系的原点，点
坐标为
，点
的坐标为
，且
，
满足
，点
在第一象限内，点
从原点出发，以每秒2个单位长度的速度沿着
的线路移动．
（1）点的坐标为___________；
（2）当点移动4秒时，请指出点的位置，并求出点的坐标；
（3）在移动过程中，当点到
轴的距离为5个单位长度时，求点移动的时间．
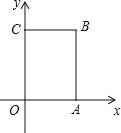
【答案】（1）(4,6)；（2）(2,6)；（3）2.5秒或5.5秒．
【解析】
（1）根据
，可以求得
、
的值，根据长方形的性质，可以求得点
的坐标；
（2）根据题意点
从原点出发，以每秒2个单位长度的速度沿着
的线路移动，可以得到当点移动4秒时，点的位置和点的坐标；
（3）由题意可以得到符合要求的有两种情况，分别求出两种情况下点移动的时间即可．
解：（1）
、满足，
，
，
解得
，
，
点的坐标是
，
故答案是：；
（2）
点从原点出发，以每秒2个单位长度的速度沿着的线路移动，
，
，
，
当点移动4秒时，在线段
上，离点
的距离是：
，
即当点移动4秒时，此时点在线段上，离点的距离是2个单位长度，点的坐标是
；
（3）由题意可得，在移动过程中，当点到
轴的距离为5个单位长度时，存在两种情况，
第一种情况，当点在
上时，
点移动的时间是：
秒，
第二种情况，当点在
上时．
点移动的时间是：
秒，
故在移动过程中，当点到轴的距离为5个单位长度时，点移动的时间是2.5秒或5.5秒．
练习册系列答案
走进文言文系列答案
相关题目
