Question

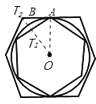
【题目】如图，有一个圆O和两个正六边形T1，T2． T1的6个顶点都在圆周上，T2的6条边都和圆O相切（我们称T1，T2分别为圆O的内接正六边形和外切正六边形）．

（1）设T1，T2的边长分别为a，b，圆O的半径为r，求r：a及r：b的值；

（2）求正六边形T1，T2的面积比S1：S2的值．

Answer 1

【答案】（1）：2（2）3：4

【解析】

根据题意画出图形，连接OE、OG，OF，由正六边形T1，得到∠EOF为60°，从而得到△EOF为等边三角形，即a=r，故得到a：r=1：1；在Rt△EOG中，由OG为角平分线，得到∠EOG=30°，利用特殊角的三角函数可求出OE及OG的长，即为r：b的比值，然后求出a：b的比值，根据正六边形T1，T2相似，其面积之比等于边长之比的平方，即可求出面积之比．

（1）连接圆心O和T1的6个顶点可得6个全等的正三角形．

所以r：a=1：1；

连接圆心O和T2相邻的两个顶点，得以圆O半径为高的正三角形，

所以r：b=AO：BO=sin60°=：2；

（2）T1：T2的边长比是：2，所以S1：S2=（a：b）2=3：4．