题目内容
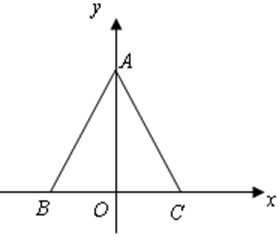
将等边三角形ABC放置在如上中图的平面直角坐标系中,已知其边长为2,现将该三角形绕点C按顺时针方向旋转90°,则旋转后点A的对应点A’的坐标为( )

A.(1+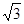 ,1) ,1) | B.(﹣1,1-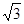 ) ) | C.(﹣1,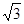 -1) -1) | D.(2,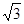 ) ) |
A.
试题分析:∵△ABC为等边三角形,
∴CA=CB=AB=2,∠CAB=∠CBA=∠BCA=60°,
如图过A′作A′D⊥x轴,垂足为D.则∠A′CD=30°,CA′=2
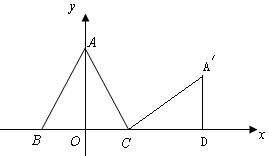
由勾股定理知:A′D=1,CD=
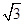 ,
,∴OD=1+
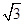
∴A′的坐标为(1+
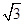 ,1)
,1)故选A.
考点: 1.坐标与图形变化-旋转;2.等边三角形的性质.

练习册系列答案
相关题目
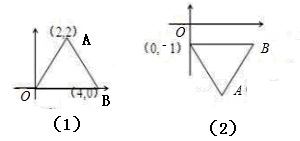

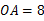 ,
,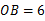 ,∠
,∠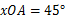 ,∠
,∠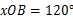 ,求
,求 、
、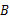 两点的坐标.
两点的坐标.