题目内容
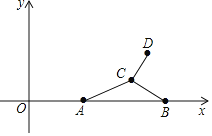
【题目】如图,在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(10,0),点C为平面上一动点,连接CA,CB,将线段CB绕点C逆时针旋转90°得到线段CD,当AC=4,线段AD的长取最大值时,点D的坐标为_____.
【答案】(4,6+4![]() ).
).
【解析】
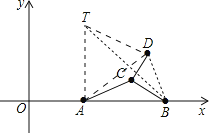
作TA⊥AB,使得TA=AB.连接AD,BT,BD.首先证明点D的运动轨迹是以T为圆心4![]() 为半径的圆,推出当点D在AT的延长线上时,AD的值最大.
为半径的圆,推出当点D在AT的延长线上时,AD的值最大.
作TA⊥AB,使得TA=AB.连接AD,BT,BD.
∵△ATB,△CDB都是等腰直角三角形,
∴BT=![]() AB,BD=
AB,BD=![]() BC,∠ABT=∠CBD=45°,
BC,∠ABT=∠CBD=45°,
∴![]() ,∠ABC=∠TBD,
,∠ABC=∠TBD,
∴△ABC∽△TBD,
∴![]() ,
,
∵A(4,0),B(10,0),AC=4,
∴AT=AB=6,DT=4![]() ,
,
∴T(4,6),
∴点D的运动轨迹是以T为圆心4![]() 为半径的圆,
为半径的圆,
∴当点D在AT的延长线上时,AD的值最大,最大值=6+4![]() ,
,
∴点D的坐标为(4,6+4![]() ) .
) .
故答案为:(4,6+4![]() ).
).

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
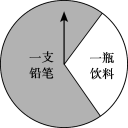
全能闯关100分系列答案【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
【题目】4月23日是世界读书日,某校为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:![]() )
)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 |
|
|
(1)![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ;
(3)如果该校现有学生400人,估计等级为“![]() ”的学生有多少名?
”的学生有多少名?