题目内容
【题目】请阅读下列材料：
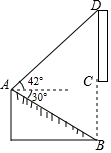
问题：如图（1），一圆柱的高为5dm，底面半径为5dm，BC是底面直径，求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线．小明设计了两条路线：
路线1：侧面展开图中的AC．如下图（2）所示：
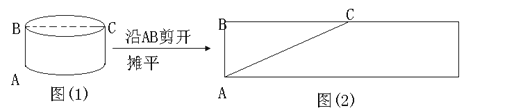
设路线1的长度为
，则
，
路线2：高线AB + 底面直径BC．如上图（1）所示：
设路线2的长度为
，则
，
∵
，
∴
∴
，
所以要选择路线2较短．
（1）小明对上述结论有些疑惑，于是他把条件改成：“圆柱的底面半径为1dm，高AB为5dm”继续按前面的路线进行计算．请你帮小明完成下面的计算：
路线1：
___________________；
路线2：
__________
∵
，
∴ (填>或<) 所以应选择路线_________(填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时，应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短．
【答案】（1）25+π2；49；＜；＜；1；（2）（2）当r＜
，l1＜l2；当r=，l1=l2；当r＞，l1＞l2．
【解析】
（1）根据勾股定理易得路线1：l12=AC2=高2+底面周长一半2；路线2：l22=(高+底面直径)2，然后比较即可；
（2）先分别求出l12和l22的值，进而得出l12-l22的值，然后分三种情况计算即可．
解：（1）路线1：l12=AC2=25+π2；
路线2：l22=(AB+BC)2=49．
∵l12＜l22，
∴l1＜l2，
∴选择路线1较短．
故答案为：25+π2；49；＜；＜；1；
（2）l12=AC2=AB2+BC2=h2+(πr)2，
l22=(AB+BC)2=(h+2r)2，
∴l12-l22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h]，
当r[(π2-4)r-4h]＜0时，r＜，此时l12＜l22，即l1＜l2；
当r[(π2-4)r-4h]=0时，r=，此时l12=l22，即l1=l2；
当r[(π2-4)r-4h]＞0时，r＞，此时l12＞l22，即l1＞l2；
综上可知：当r＜，l1＜l2；当r=，l1=l2；当r＞，l1＞l2．
