ЬтФПФкШн
ЁОЬтФПЁПФГЩЬГЁгавЛИіПЩвдздгЩзЊЖЏЕФдВаЮзЊХЬЃЈШчЭМЃЉЃЎЙцЖЈЃКЙЫПЭЙКЮя100дЊвдЩЯПЩвдЛёЕУвЛДЮзЊЖЏзЊХЬЕФЛњЛсЃЌЕБзЊХЬЭЃжЙЪБЃЌжИеыТфдкФФвЛИіЧјгђОЭЛёЕУЯргІЕФНБЦЗЃЈжИеыжИЯђСНИіЩШаЮЕФНЛЯпЪБЃЌЕБзїжИЯђгвБпЕФЩШаЮЃЉЃЎЯТБэЪЧЛюЖЏНјаажаЕФвЛзщЭГМЦЪ§ОнЃК
зЊЖЏзЊХЬЕФДЮЪ§n | 100 | 150 | 200 | 500 | 800 | 1000 |
ТфдкЁАЧІБЪЁБЕФДЮЪ§m | 68 | 111 | 136 | 345 | 546 | 701 |
ТфдкЁАЧІБЪЁБЕФЦЕТЪ ЃЈНсЙћБЃСєаЁЪ§ЕуКѓСНЮЛЃЉ | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
ЃЈ1ЃЉзЊЖЏИУзЊХЬвЛДЮЃЌЛёЕУЧІБЪЕФИХТЪдМЮЊ_______ЃЛЃЈНсЙћБЃСєаЁЪ§ЕуКѓвЛЮЛЃЉ
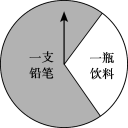
ЃЈ2ЃЉЧІБЪУПжЛ0.5дЊЃЌвћСЯУПЦП3дЊЃЌОЭГМЦИУЩЬГЁУПЬьдМга4000УћЙЫПЭВЮМгГщНБЛюЖЏЃЌЧыМЦЫуИУЩЬГЁУПЬьашвЊжЇГіЕФНБЦЗЗбгУЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌИУЩЬГЁЯыАбУПЬьжЇГіЕФНБЦЗЗбгУПижЦдк3000дЊзѓгвЃЌдђзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊ______ЖШЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0.7ЃЛЃЈ2ЃЉИУЩЬГЁУПЬьДѓжТашвЊжЇГіЕФНБЦЗЗбгУЮЊ5000дЊЃЛЃЈ3ЃЉ36
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЦЕТЪЙРМЦИХТЪЧѓНтЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉЕУЕНЛёЕУЧІБЪЕФИХТЪЮЊ0.7КЭЛёЕУвћСЯЕФИХТЪЮЊ0.3ЃЌШЛКѓМЦЫу4000ЁС0.5ЁС0.7+4000ЁС3ЁС0.3МДПЩЃЛ
ЃЈ3ЃЉЩшзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊnЖШЃЌдђ4000ЁС3ЁС![]() +4000ЁС0.5ЃЈ1-
+4000ЁС0.5ЃЈ1-![]() ЃЉ=3000ЃЌШЛКѓНтЗНГЬМДПЩЃЎ
ЃЉ=3000ЃЌШЛКѓНтЗНГЬМДПЩЃЎ
ЃЈ1ЃЉзЊЖЏИУзЊХЬвЛДЮЃЌЛёЕУЧІБЪЕФИХТЪдМЮЊ0.7ЃЛ
ЙЪД№АИЮЊ: 0.7
ЃЈ2ЃЉ4000ЁС0.5ЁС0.7+4000ЁС3ЁС0.3ЃН5000ЃЌ
ЫљвдИУЩЬГЁУПЬьДѓжТашвЊжЇГіЕФНБЦЗЗбгУЮЊ5000дЊЃЛ
ЃЈ3ЃЉЩшзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊnЖШЃЌ
дђ4000ЁС3ЁС![]() +4000ЁС0.5ЃЈ1Љ
+4000ЁС0.5ЃЈ1Љ![]() ЃЉЃН3000ЃЌНтЕУnЃН36ЃЌ
ЃЉЃН3000ЃЌНтЕУnЃН36ЃЌ
ЫљвдзЊХЬЩЯЁАвЛЦПвћСЯЁБЧјгђЕФдВаФНЧгІЕїећЮЊ36ЖШЃЎ
ЙЪД№АИЮЊ36ЃЎ