Question

【题目】已知直线y=kx+b交x轴于点A(1，0) ，与双曲线 交于点

（1）求直线AB的解析式为____ ____________；

（2）若 x 轴上存在动点 M（m，0），过点 M 且与 x 轴垂直的直线与直线AB交于点C，与双曲线交于点D(C、D两点不重合），当BC >BD时，写出m的取值范围_____________．

Answer 1

【答案】（1）y=-x+1；（2）m<-2_或_ m>2

【解析】

（1）将点B（-1，a）代入，求出a，再将A、B两点的坐标代入y=kx+b，利用待定系数法即可求出直线AB的解析式；

（2）过点B作BE⊥CD于点E．根据三角形中，两条边在第三边上的射影长之间关系，若存在动点M(m,0)，满足BC>BD，则有CE>DE. 由题意得出C（m，-m+1），D（m，），根据点E与点B的纵坐标相同得到E(m,2),得到CE= ， DE=，列不等式，分C在D的上方和C在D的下方两种情况，数形结合，解不等式即可得其范围.

解：（1）∵点B（-1，a）在双曲线上，

∴a=2，

∴B（-1，2）．

又∵直线y=kx+b过点A、B，

∴，

解得，

∴直线AB的解析式为：y=-x+1；

（2）

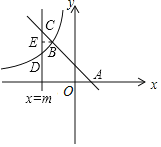
过点B作BE⊥CD于点E．

∵BC>BD，

∴CE>DE

由题意可知，C（m，-m+1），D（m，）,E（m，2），

CE=， DE=，

∴ >

当m>0时，>，解得m>2，

当m<0时，由图可知，m<-1,又<-()，解得m<-2

综上：m<-2或 m>2