题目内容
【题目】点![]() 为图形
为图形![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 直线
直线![]() 垂足为
垂足为![]() ,记
,记![]() 的长度为
的长度为![]() .
.
定义一:若![]() 存在最大值,则称其为“图形
存在最大值,则称其为“图形![]() 到直线
到直线![]() 的限距离”,记作
的限距离”,记作![]() ;
;
定义二:若![]() 存在最小值,则称其为“图形
存在最小值,则称其为“图形![]() 到直线
到直线![]() 的基距离”,记作
的基距离”,记作![]() ;
;
(1)已知直线![]() ,平面内反比例函数
,平面内反比例函数![]() 在第一象限内的图象记作
在第一象限内的图象记作![]() 则
则![]() .
.
(2)已知直线![]() ,点
,点![]() ,点
,点![]() 是
是![]() 轴上一个动点,
轴上一个动点,![]() 的半径为
的半径为![]() ,点
,点![]() 在
在![]() 上,若
上,若![]() 求此时
求此时![]() 的取值范围,
的取值范围,
(3)已知直线![]() 恒过定点
恒过定点![]() ,点
,点![]() 恒在直线
恒在直线![]() 上,点
上,点![]() 是平面上一动点,记以点
是平面上一动点,记以点![]() 为顶点,原点为对角线交点的正方形为图形
为顶点,原点为对角线交点的正方形为图形![]()
![]() ,若请直接写出
,若请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)作直线:![]() 平行于直线
平行于直线![]() ,且与H相交于点P,连接PO并延长交直线
,且与H相交于点P,连接PO并延长交直线![]() 于点Q,作PM⊥x轴,根据只有一个交点可求出b,再联立求出P的坐标,从而判断出PQ平分∠AOB,再利用直线
于点Q,作PM⊥x轴,根据只有一个交点可求出b,再联立求出P的坐标,从而判断出PQ平分∠AOB,再利用直线![]() 表达式求A、B坐标证明OA=OB,从而证出PQ即为最小距离,最后利用勾股定理计算即可;
表达式求A、B坐标证明OA=OB,从而证出PQ即为最小距离,最后利用勾股定理计算即可;
(2)过点![]() 作
作![]() 直线
直线![]() ,可判断出
,可判断出![]() 上的点到直线
上的点到直线![]() 的最大距离为
的最大距离为![]() ,然后根据最大距离的范围求出TH的范围,从而得到FT的范围,根据范围建立不等式组求解即可;
,然后根据最大距离的范围求出TH的范围,从而得到FT的范围,根据范围建立不等式组求解即可;
(3)把点P坐标带入表达式,化简得到关于a、b的等式,从而推出直线![]() 的表达式,根据点E的坐标可确定点E所在直线表达式,再根据最小距离为0,推出直线
的表达式,根据点E的坐标可确定点E所在直线表达式,再根据最小距离为0,推出直线![]() 一定与图形K相交,从而分两种情况画图求解即可.
一定与图形K相交,从而分两种情况画图求解即可.
解:(1)作直线:![]() 平行于直线
平行于直线![]() ,且与H相交于点P,连接PO并延长交直线
,且与H相交于点P,连接PO并延长交直线![]() 于点Q,作PM⊥x轴,
于点Q,作PM⊥x轴,
∵ 直线:![]() 与H相交于点P,
与H相交于点P,
∴![]() ,即
,即![]() ,只有一个解,
,只有一个解,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
联立 ,解得
,解得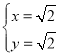 ,即
,即![]() ,
,
∴![]() ,且点P在第一、三象限夹角的角平分线上,即PQ平分∠AOB,
,且点P在第一、三象限夹角的角平分线上,即PQ平分∠AOB,
∴![]() 为等腰直角三角形,且OP=2,
为等腰直角三角形,且OP=2,
∵直线![]() :
:![]() ,
,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴A(-2,0),B(0,-2),
∴OA=OB=2,
又∵OQ平分∠AOB,
∴OQ⊥AB,即PQ⊥AB,
∴PQ即为H上的点到直线![]() 的最小距离,
的最小距离,
∵OA=OB,
∴![]() ,
,
∴AQ=OQ,
∴在![]() 中,OA=2,则OQ=
中,OA=2,则OQ=![]() ,
,
∴![]() ,即
,即![]() ;
;

(2)由题过点![]() 作
作![]() 直线
直线![]() ,
,
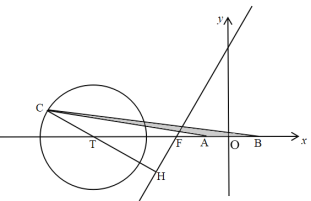
则![]() 上的点到直线
上的点到直线![]() 的最大距离为
的最大距离为![]() ,
,
∵![]() ,
,
即![]() ,
,
∴![]() ,
,
由题![]() ,则
,则![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() ;
;
(3)∵直线![]() 恒过定点
恒过定点![]() ,
,
∴把点P代入得:![]() ,
,
整理得:![]() ,
,
∴![]() ,化简得
,化简得![]() ,
,
∴![]() ,
,
又∵点![]() 恒在直线
恒在直线![]() 上,
上,
∴直线![]() 的表达式为:
的表达式为:![]() ,
,
∵![]() ,
,
∴直线![]() 一定与以点
一定与以点![]() 为顶点,原点为对角线交点的正方形图形相交,
为顶点,原点为对角线交点的正方形图形相交,
∵![]() ,
,
∴点E一定在直线![]() 上运动,
上运动,
情形一:如图,当点E运动到所对顶点F在直线![]() 上时,由题可知E、F关于原点对称,
上时,由题可知E、F关于原点对称,
∵![]() ,
,
∴![]() ,
,
把点F代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∵当点E沿直线向上运动时,对角线变短,正方形变小,无交点,
∴点E要沿直线向下运动,即![]() ;
;
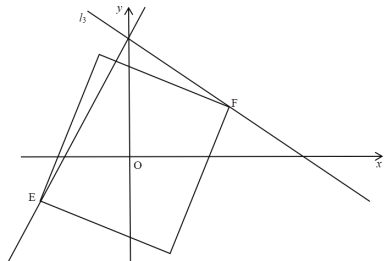
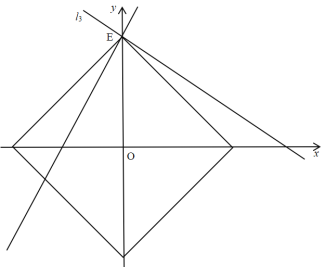
情形二:如图,当点E运动到直线![]() 上时,
上时,
把点E代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∵当点E沿直线向下运动时,对角线变短,正方形变小,无交点,
∴点E要沿直线向上运动,即![]() ,
,
综上所述,![]() 或
或![]() .
.

【题目】为了解九年级学生体育水平,学校对九年级全体学生进行了体育测试,并从甲、乙两班中各随机抽取![]() 名学生成绩(满分
名学生成绩(满分![]() 分)进行整理分析(成绩得分用
分)进行整理分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]()
![]() ;
;![]()
![]() ,
,![]()
![]() )下面给出了部分信息:
)下面给出了部分信息:
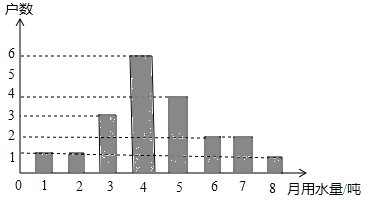
甲班![]() 名学生体育成绩:
名学生体育成绩:![]()
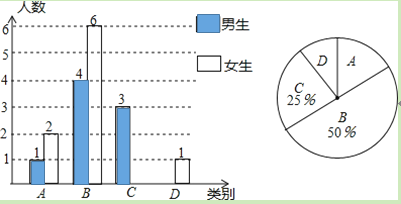
乙班![]() 名学生体育成绩在
名学生体育成绩在![]() 组中的数据是:
组中的数据是: ![]()
甲、乙两班被抽取学生体育成绩统计表
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
|
|
|
乙班 |
|
|
|
|
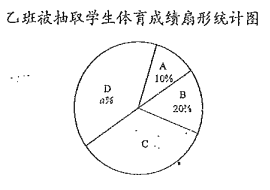
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 根据以上数据,你认为 班(填“甲”或“乙”)体育水平更高,说明理由(两条理由):
根据以上数据,你认为 班(填“甲”或“乙”)体育水平更高,说明理由(两条理由):
![]() ;
;
![]() .
.
![]() 学校九年级学生共
学校九年级学生共![]() 人,估计全年级体育成绩优秀
人,估计全年级体育成绩优秀![]() 的学生人数是多少?
的学生人数是多少?