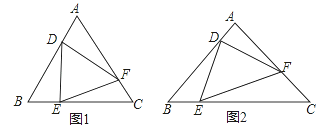
题目内容
【题目】已知:如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]()
(1)求证:![]() ; (2)求证:
; (2)求证:![]() ;
;
(3)取![]() 边的中点
边的中点![]() ,连结
,连结![]() 、
、![]() 、
、![]() ,取
,取![]() 的中点G,连结
的中点G,连结![]() ,说明GH与DE的位置关系.
,说明GH与DE的位置关系.

【答案】(1)见解析;(2)见解析;(3)GH⊥DE,理由见解析.
【解析】
(1)根据等腰直角三角形的性质可得DB=DC,根据同角的余角相等可得∠DBF=∠ACD,然后利用ASA证明△ADC≌△FDB即可得到BF=AC;
(2)根据等角的余角相等可得∠A=∠BCA,进而得到BA=BC,根据等腰三角形的性质(三线合一),可得AE=EC=![]() AC=
AC=![]() BF;
BF;
(3)根据直角三角形斜边上的中线等于斜边的一半可证明DH=EH,然后根据等腰三角形的性质(三线合一)可得结论.
(1)∵∠ABC=45°,CD⊥AB于D,
∴∠DBC=∠DCB=45°,
∴DB=DC,
∵BE⊥AC,
∴∠AEB=∠ADC=90°,
∴∠A+∠ABE=90°,∠A+ACD=90°,
∴∠DBF=∠ACD,
在△ADC和△FDB中,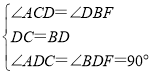 ,
,
∴△ADC≌△FDB(ASA),
∴BF=AC;
(2)∵∠ABE=∠CBE,∠ABE+∠A=90°,∠CBE+∠BCA=90°,
∴∠A=∠BCA,
∴BA=BC,
∵BE⊥AC,
∴AE=CE,
∵AC=BF,
∴CE=![]() BF;
BF;
(3)GH⊥DE,
理由:如图,
∵在Rt△BDC和Rt△BEC中,H为BC中点,
∴DH=![]() BC,EH=
BC,EH=![]() BC,
BC,
∴DH=EH,
∵G为DE中点,
∴GH⊥DE.

练习册系列答案
相关题目