题目内容
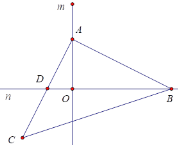
【题目】如图,直线m⊥n,等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是m、n上两个动点,直角边AC交直线n于点D,斜边BC交直线m于点E.
(1)如图(1)求证:∠DAO=∠ABO;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3),分别以OB、AB为直角边作等腰直角△BOD和等腰直角△ABC,连结CD交直线n于点P,求![]() 的值.
的值.


【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据题意可得∠ABO+∠BAO=90°,∠DAO+∠BAO=90°,利用同角的余角相等可得结论;
(2)作CG⊥AC交m与点G,首先利用ASA证明△ADB≌△CGA,可得AD=CG,进而得到CG=CD,然后证明△DCE≌△GCE,可得∠CDE=∠CGE,等量代换即可得到结论;
(3)作CF⊥n于点F,根据“一线三等角”模型易证△ABO≌△BCF,可得OB=FC,AO=BF,然后结合△BOD是等腰直角三角形证明△DBP≌△CFP,得到BP=FP,最后利用三角形面积公式计算化简即可.
解:(1)∵直线m⊥n,
∴∠AOD=∠AOB=90°,
∴∠ABO+∠BAO=90°,
∵∠BAC=90°,
∴∠DAO+∠BAO=90°,
∴∠DAO=∠ABO;
(2)作CG⊥AC交m与点G,则∠ACG=90°,
在△ADB和△CGA中, ,
,
∴△ADB≌△CGA(ASA),
∴AD=CG,
∵AD=CD,
∴CG=CD,
∵∠ACB=45°,
∴∠GCE=45°,
∴∠ACB=∠GCE,
又∵CE=CE,
∴△DCE≌△GCE(SAS),
∴∠CDE=∠CGE,
∵△ADB≌△CGA,
∵∠CGE=∠ADB,
∴∠ADB=∠CDE;

(3)作CF⊥n于点F,则∠CFB=90°,
∴∠CBF+∠BCF=90°,
∵△ABC是等腰直角三角形,
∴∠ABC=90°,AB=BC,
∴∠ABO+∠CBF=90°,
∴∠BCF=∠ABO,
在△ABO和△BCF中,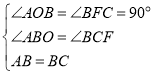 ,
,
∴△ABO≌△BCF(AAS),
∴OB=FC,AO=BF,
∵△BOD是等腰直角三角形,
∴OB=BD,∠OBD=∠DBP=90°,
∴BD=FC,
在△DBP和△CFP中, ,
,
∴△DBP≌△CFP(AAS),
∴BP=FP,
∴ .
.


【题目】“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
(1)这组数据的众数是 ,中位数是 .
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.








