Question

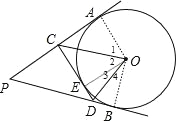
【题目】如图，P是⊙O外一动点，PA、PB、CD是⊙O的三条切线，C、D分别在PA、PB上，连接OC、OD．设∠P为x°，∠COD为y°，则y随x的函数关系图象为（ ）

A. B.

C. D.

Answer 1

【答案】B

【解析】如图，设CD与⊙O相切于点E，连结OA、OB、OE， 根据切线长定理由PA、PB、CD是⊙O的三条切线，可得CA=CE，DE=DB，OA⊥PA，OB⊥PB，OE⊥CD，然后根据角平分线的判定，可得OC平分∠AOE，OD平分∠BOE，进而由角平分线的性质可得∠1=∠2，∠3=∠4，可知∠COD=∠2+∠3=∠AOB，最后由题意知∠AOB=180°﹣∠P=180°﹣x°，所以y=90°﹣x（0＜x＜180°）．

故选：B．