Question

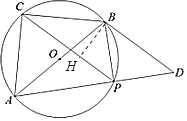
【题目】如图，△ABC是等腰直角三角形，且AC=BC，P是△ABC外接圆⊙O上的一动点（点P与点C位于直线AB的异侧）连接AP、BP，延长AP到D，使PD=PB，连接BD．

（1）求证：PC∥BD；

（2）若⊙O的半径为2，∠ABP=60°，求CP的长；

（3）随着点P的运动，的值是否会发生变化，若变化，请说明理由；若不变，请给出证明．

Answer 1

【答案】（1）证明见解析；（2）+；（3）的值不变，.

【解析】

（1）根据等腰三角形的性质得到∠ABC=45°，∠ACB=90°，根据圆周角定理得到∠APB=90°，得到∠APC=∠D，根据平行线的判定定理证明；

（2）作BH⊥CP，根据正弦、余弦的定义分别求出CH、PH，计算即可；

（3）证明△CBP∽△ABD，根据相似三角形的性质解答．

（1）证明：∵△ABC是等腰直角三角形，且AC=BC，

∴∠ABC=45°，∠ACB=90°，

∴∠APC=∠ABC=45°，

∴AB为⊙O的直径，

∴∠APB=90°，

∵PD=PB，

∴∠PBD=∠D=45°，

∴∠APC=∠D=45°，

∴PC∥BD；

（2）作BH⊥CP，垂足为H，

∵⊙O的半径为2，∠ABP=60°，

∴BC=2，∠BCP=∠BAP=30°，∠CPB=∠BAC=45°，

在Rt△BCH中，CH=BCcos∠BCH=，

BH=BCsin∠BCH=，

在Rt△BHP中，PH=BH=，

∴CP=CH+PH=+；

（3）的值不变，

∵∠BCP=∠BAP，∠CPB=∠D，

∴△CBP∽△ABD，

∴=，

∴=，即=．