题目内容
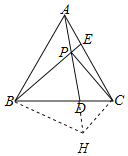
【题目】如图,等边△ABC中,点D、E分别在边BC、AC上,AE=CD,连接AD、BE交于点P.
(1)求证:∠BPD=60°.
(2)连接PC,若CP⊥PB.当AP=3,求BP的长.

【答案】(1)详见解析;(2)6.
【解析】
(1)证明△ADC≌△BEA即可说明AD=BE;证明∠BPQ=∠EBA+∠BAP=60°即可求解∠PBQ的度数;
(2)延长PD至H,使PH=BP,连接BH、CH,证明△BPH是等边三角形,得出BP=BH=PH,∠HBP=∠ABD=60°,推出∠ABP=∠CBH,由SAS证得△ABP≌△CBH得出CH=AP=3,∠BCH=∠BAP,证明CH∥BE,推出CH⊥CP,∠HPC=30°,得出PH=2CH=6,即可得出结果.
(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
在△ABE和△CAD中,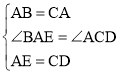 ,
,
∴△ABE≌△CAD(SAS),
∴∠ABE=∠CAD,
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°,
∴∠BPD=∠ABE+∠BAD=60°;
(2)解:延长PD至H,使PH=BP,连接BH、CH,如图所示:
∵△ABC是等边三角形,
∴AB=BC,∠BAC=∠ABC=60°,
由(1)知:∠BPD=60°,
∴△BPH是等边三角形,
∴BP=BH=PH,∠HBP=∠ABD=60°,
∴∠ABP+∠PBD=∠CBH+∠PBD,
∴∠ABP=∠CBH,
在△ABP和△CBH中,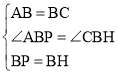 ,
,
∴△ABP≌△CBH(SAS),
∴CH=AP=3,∠BCH=∠BAP,
∵∠ABE=∠CAD,∠BAC=∠ABC=60°,
∴∠EBC=∠BAP,
∴∠BCH=∠EBC,
∴CH∥BE,
∵CP⊥PB,∠BPD=60°,
∴CH⊥CP,∠HPC=90°﹣60°=30°,
∴PH=2CH=2×3=6,
∴BP=6.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案