ĢāÄæÄŚČŻ
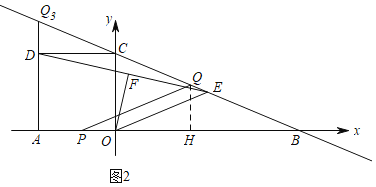
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļß![]() ·Ö±š½»xÖį”¢yÖįÓŚµćB£¬C£¬Õż·½ŠĪAOCDµÄ¶„µćDŌŚµŚ¶žĻóĻŽÄŚ£¬EŹĒBCÖŠµć£¬OF”ĶDEÓŚµćF£¬Į¬½įOE£¬¶ÆµćPŌŚAOÉĻ“ÓµćAĻņÖÕµćOŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±£¬¶ÆµćQŌŚÖ±ĻßBCÉĻ“ÓijµćQ1ĻņÖÕµćQ2ŌČĖŁŌĖ¶Æ£¬ĖüĆĒĶ¬Ź±µ½“ļÖÕµć£®
·Ö±š½»xÖį”¢yÖįÓŚµćB£¬C£¬Õż·½ŠĪAOCDµÄ¶„µćDŌŚµŚ¶žĻóĻŽÄŚ£¬EŹĒBCÖŠµć£¬OF”ĶDEÓŚµćF£¬Į¬½įOE£¬¶ÆµćPŌŚAOÉĻ“ÓµćAĻņÖÕµćOŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±£¬¶ÆµćQŌŚÖ±ĻßBCÉĻ“ÓijµćQ1ĻņÖÕµćQ2ŌČĖŁŌĖ¶Æ£¬ĖüĆĒĶ¬Ź±µ½“ļÖÕµć£®
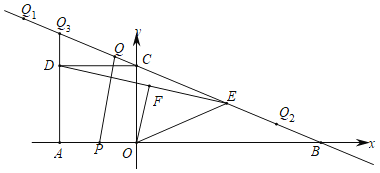
£Ø1£©ĒóµćBµÄ×ų±źŗĶOEµÄ³¤£»
£Ø2£©ÉčµćQ2ĪŖ(m£¬n)£¬µ±![]() tan”ĻEOFŹ±£¬ĒóµćQ2µÄ×ų±ź£»
tan”ĻEOFŹ±£¬ĒóµćQ2µÄ×ų±ź£»
£Ø3£©øł¾Ż£Ø2£©µÄĢõ¼ž£¬µ±µćPŌĖ¶Æµ½AOÖŠµćŹ±£¬µćQĒ”ŗĆÓėµćCÖŲŗĻ£®
¢ŁŃÓ³¤AD½»Ö±ĻßBCÓŚµćQ3£¬µ±µćQŌŚĻ߶ĪQ2Q3ÉĻŹ±£¬ÉčQ3Q£½s£¬AP£½t£¬Ēós¹ŲÓŚtµÄŗÆŹż±ķ“ļŹ½£®
¢Śµ±PQÓė”÷OEFµÄŅ»±ßĘ½ŠŠŹ±£¬ĒóĖłÓŠĀś×ćĢõ¼žµÄAPµÄ³¤£®
”¾“š°ø”æ£Ø1£©£Ø8£¬0£©£¬![]() £»£Ø2£©£Ø6£¬1£©£»£Ø3£©¢Ł
£»£Ø2£©£Ø6£¬1£©£»£Ø3£©¢Ł![]() £¬¢Ś
£¬¢Ś![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() »ņ
»ņ![]() .
.
”¾½āĪö”æ
£Ø1£©Įīy£½0£¬æɵĆBµÄ×ų±ź£¬ĄūÓĆ¹“¹É¶ØĄķæɵĆBCµÄ³¤£¬¼“æɵƵ½OE£»
£Ø2£©ČēĶ¼£¬×÷øØÖśĻߣ¬Ö¤Ć÷”÷CDN”×”÷MEN£¬µĆCN£½MN£½1£¬¼ĘĖćENµÄ³¤£¬øł¾ŻĆ껿·ØæɵĆOFµÄ³¤£¬ĄūÓĆ¹“¹É¶ØĄķµĆOFµÄ³¤£¬ÓÉ![]() ŗĶ
ŗĶ![]() £¬æÉµĆ½įĀŪ£»
£¬æÉµĆ½įĀŪ£»
£Ø3£©¢ŁĻČÉčs¹ŲÓŚt³ÉŅ»“ĪŗÆŹż¹ŲĻµ£¬Éčs£½kt£«b£¬øł¾Żµ±µćPŌĖ¶Æµ½AOÖŠµćŹ±£¬µćQĒ”ŗĆÓėµćCÖŲŗĻ£¬µĆt£½2Ź±£¬CD£½4£¬DQ3£½2£¬s£½![]() £¬øł¾ŻQ3£Ø4£¬6£©£¬Q2£Ø6£¬1£©£¬æɵĆt£½4Ź±£¬s£½
£¬øł¾ŻQ3£Ø4£¬6£©£¬Q2£Ø6£¬1£©£¬æɵĆt£½4Ź±£¬s£½![]() £¬ĄūÓĆ“ż¶ØĻµŹż·ØæɵĆs¹ŲÓŚtµÄŗÆŹż±ķ“ļŹ½£»
£¬ĄūÓĆ“ż¶ØĻµŹż·ØæɵĆs¹ŲÓŚtµÄŗÆŹż±ķ“ļŹ½£»
¢Ś·ÖČżÖÖĒéæö£ŗ
£Øi£©µ±PQ”ĪOEŹ±£¬øł¾Ż![]() £¬±ķŹ¾BHµÄ³¤£¬øł¾ŻAB£½12£¬ĮŠ·½³ĢæɵĆtµÄÖµ£»
£¬±ķŹ¾BHµÄ³¤£¬øł¾ŻAB£½12£¬ĮŠ·½³ĢæɵĆtµÄÖµ£»
£Øii£©µ±PQ”ĪOFŹ±£¬øł¾Żtan”ĻHPQ£½tan”ĻCDN£½![]() £¬ĮŠ·½³ĢĪŖ2t2£½
£¬ĮŠ·½³ĢĪŖ2t2£½![]() (7
(7![]() t)£¬æɵĆtµÄÖµ£®
t)£¬æɵĆtµÄÖµ£®
£Øiii£©ÓÉĶ¼ŠĪæÉÖŖPQ²»æÉÄÜÓėEFĘ½ŠŠ£®
½ā£ŗ£Ø1£©Įī![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() ĪŖ
ĪŖ![]() .
.
”ß![]() ĪŖ
ĪŖ![]() £¬
£¬
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() .
.
ÓÖ”ß![]() ĪŖ
ĪŖ![]() ÖŠµć£¬”ą
ÖŠµć£¬”ą![]() .
.
£Ø2£©ČēĶ¼£¬×÷![]() ÓŚµć
ÓŚµć![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() .
.
”ß![]() £¬
£¬
”ą![]() £¬
£¬
Óɹ“¹É¶ØĄķµĆ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() .
.
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() ĪŖ
ĪŖ![]() .
.
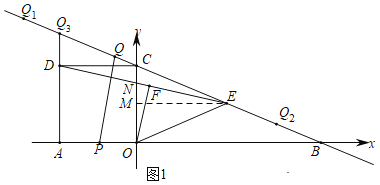
£Ø3£©¢Ł”߶Ƶć![]() Ķ¬Ź±×÷ŌČĖŁÖ±ĻßŌĖ¶Æ£¬
Ķ¬Ź±×÷ŌČĖŁÖ±ĻßŌĖ¶Æ£¬
”ą![]() ¹ŲÓŚ
¹ŲÓŚ![]() ³ÉŅ»“ĪŗÆŹż¹ŲĻµ£¬Éč
³ÉŅ»“ĪŗÆŹż¹ŲĻµ£¬Éč![]() £¬
£¬
½«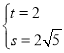 ŗĶ
ŗĶ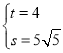 “śČėµĆ
“śČėµĆ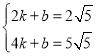 £¬½āµĆ
£¬½āµĆ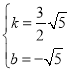 £¬
£¬
”ą![]() .
.
¢Ś£Ø¢”£©µ±![]() Ź±£¬£ØČēĶ¼£©£¬
Ź±£¬£ØČēĶ¼£©£¬![]() £¬
£¬
×÷![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬Ōņ
£¬Ōņ![]() .
.
ӧ![]()
![]() £¬
£¬
ÓÖ”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() .
.
£Ø¢¢£©µ±![]() Ź±£ØČēĶ¼£©£¬¹żµć
Ź±£ØČēĶ¼£©£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬ÓÉ
£¬ÓÉ![]() µĆ
µĆ![]() .
.
ӧ![]() ,
,
”ą![]() ,
,
”ą![]()
![]() £¬
£¬
”ą![]() .
.
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() .
.
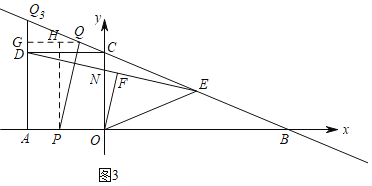
£Ø¢££©ÓÉĶ¼ŠĪæÉÖŖ![]() ²»æÉÄÜÓė
²»æÉÄÜÓė![]() Ę½ŠŠ.
Ę½ŠŠ.
×ŪÉĻĖłŹö£¬µ±![]() Óė
Óė![]() µÄŅ»±ßĘ½ŠŠŹ±£¬
µÄŅ»±ßĘ½ŠŠŹ±£¬![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() »ņ
»ņ![]() .
.