题目内容
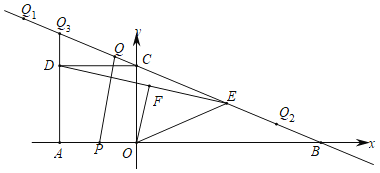
【题目】如图,抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线解析式;
(2)若点![]() 在第一象限内,当
在第一象限内,当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(3)将![]() 绕平面直角坐标系中某点逆时针旋转
绕平面直角坐标系中某点逆时针旋转![]() ,对应点为
,对应点为![]() ,
,![]() ,
,![]() ,当
,当![]() 中有两个顶点落在抛物线上时,直接写出
中有两个顶点落在抛物线上时,直接写出![]() 的坐标.
的坐标.
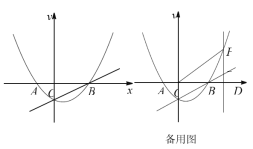
【答案】(1)![]() ;(2)四边形
;(2)四边形![]() 的面积为
的面积为![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,A
,A![]() 在抛物线上,于是列方程即可得到结论.
在抛物线上,于是列方程即可得到结论.
(2)根据函数解析式得到![]() 和
和![]() ,求得BC的解析式为
,求得BC的解析式为![]() ,设
,设![]() ,得到
,得到![]() 和
和![]() ,根据已知条件列方程得到m=5,m=0(舍去),求得
,根据已知条件列方程得到m=5,m=0(舍去),求得![]() 、
、![]() 和
和![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
(3)分三种情况:①当点O,C的对应点O1,C1落在抛物线上时,求出C1点坐标,②当点C,B的对应点C1,B1落在抛物线上时,求出C1点坐标,③△BOC绕某点逆时针旋转![]() 后,
后,![]() 轴,此时
轴,此时![]() ,
,![]() 不会同时在抛物线上,所以
不会同时在抛物线上,所以![]() 的坐标即为①②所求.
的坐标即为①②所求.
(1)∵抛物线的对称轴为![]() ,且过点
,且过点![]()
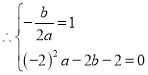
解得
![]()
(2)![]() ,对称轴
,对称轴![]() ,
,![]()
抛物线与![]() 轴交于点
轴交于点![]()
![]()
设![]()
![]()
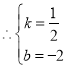
![]()
设![]() ,则
,则![]()
![]() .
.
![]()
![]()
![]() ,
,![]() (舍)
(舍)
![]() ,
,![]() ,
,![]()
![]() 四边形
四边形![]()
![]()
![]()
![]()
![]() 当
当![]() 时,四边形
时,四边形![]() 的面积为
的面积为![]()
(3)分三种情况:①当点O,C的对应点O1,C1落在抛物线上时,则O1C1//x轴
∵OC=2,抛物线的对称轴为x=1,
∴点C1的横坐标为2.
将x=2代人![]() ,得y=-2
,得y=-2
∴点C1的坐标为(2,-2);
②当点C,B的对应点C1,B1落在抛物线上时,设C1(n,![]() ),
),
∵O1C1//x轴, O1C1=OC=2
∴O1(n-2, ![]() ).
).
∵旋转后O1B1//y轴, O1B1=OB=4
∴B1(n-2,![]() ),将点B1代人抛物线
),将点B1代人抛物线![]() 得(
得(![]() ,解得n=-2.
,解得n=-2.
∴点C1的坐标为(-2,0);
③△BOC绕某点逆时针旋转![]() 后,
后,![]() 轴,此时
轴,此时![]() ,
,![]() 不会同时在抛物线上,
不会同时在抛物线上,
∴![]() 的坐标为
的坐标为![]() 或
或![]() .
.

【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:(A)和同学亲友聊天;(B)学习:(C)购物;(D)游戏;(E)其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
选项 | 频数 | 频率 |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|
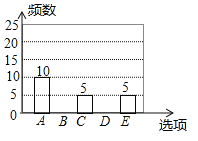
根据以上信息解答下列问题:
(1)求本次参与调查的总人数.
(2)![]() ___________,
___________,![]() ___________,
___________,![]() ___________,并补全条形统计图.
___________,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.