题目内容
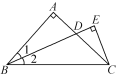
【题目】将两个直角三角尺的顶点O叠放在一起

(1)如图(1)若∠BOD=35°,则∠AOC=___;若∠AOC=135°,则∠BOD=___;
(2)如图(2)若∠AOC=140°,则∠BOD=___;
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
【答案】(1)145°,45°;(2)40°;(3)∠AOC与∠BOD互补,理由见解析
【解析】
(1)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD-∠BOD可分别计算出∠AOC、∠BOD的度数;
(2)根据∠BOD=360°-∠AOC-∠AOB-∠COD计算可得;
(3)由∠AOD+∠BOD+∠BOD+∠BOC=180°且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补;
解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD-∠BOD=90°+90°-35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD-∠AOC=90°+90°-135°=45°;
(2)如图2,若∠AOC=140°,
则∠BOD=360°-∠AOC-∠AOB-∠COD=40°;
(3)∠AOC与∠BOD互补,理由如下,
∵∠AOD+∠BOD+∠BOD+∠BOC=180°,
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.

【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.