题目内容
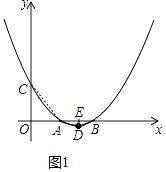
【题目】如图,在平面直角坐标系中的两点A(m,0),B(2m,0)(m>0),二次函数y=ax2+bx+m的图象与x轴交与A,B两点与y轴交于点C,顶点为点D.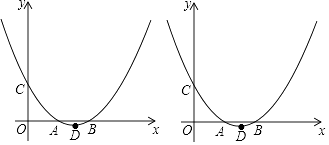
(1)当m=1时,直线BC的解析式为 , 二次函数y=ax2+bx+m的解析式为;
(2)求二次函数y=ax2+bx+m的解析式为(用含m的式子表示);
(3)连接AC、AD、BD,请你探究 ![]() 的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
(4)当m为正整数时,依次得到点A1 , A2 , …,Am的横坐标分别为1,2,…m;点B1 , B2 , …,Bm 的横坐标分别为2,4,…2m(m≤10);经过点A1 , B1 , 点A2 , B2 , …,点Am , Bm的这组抛物线y=ax2+bx+m分别与y轴交于点C1 , C2 , …,Cm , 由此得到了一组直线B1C1 , B2C2 , …,BmCm , 在点B1 , B2 , …,Bm 中任取一点Bn , 以线段OBn为边向上作正方形OBnEnFn , 若点En在这组直线中的一条直线上,直接写出所有满足条件的点En的坐标.
【答案】
(1)y=﹣ ![]() x+1,y=
x+1,y= ![]() x2﹣
x2﹣ ![]() x+1
x+1
(2)解:y= ![]() x2﹣
x2﹣ ![]() x+m
x+m
(3)解:结论: ![]() 的值与m无关.
的值与m无关.
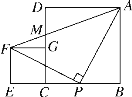
理由:如图1中,连接AC、AD、BD,作DE⊥AB于E.
∵y= ![]() x2﹣
x2﹣ ![]() x+m=
x+m= ![]() (x﹣
(x﹣ ![]() m)2﹣
m)2﹣ ![]() ,
,
∴D( ![]() m,﹣
m,﹣ ![]() ),
),
∴DE= ![]() ,
,
∵A(m,0),B(2m,0),
∴OA=m,OC=m,
∴S△AOC= ![]() m2,
m2,
∴ ![]() =
= ![]() =8,
=8,
∴ ![]() 的值与m无关
的值与m无关
(4)解:如图2中,

观察图象可知,满足条件的点E的坐标分别为:E1(2,2),E2(4,4),E3(6,6)
【解析】解:(1)m=1时,A(1,0),B(2,0),C(0,1).
设直线BC的解析式为y=kx+b,则有 ![]() ,解得
,解得 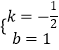 ,
,
∴直线BC的解析式为y=﹣ ![]() x+1.
x+1.
把A(1,0),B(2,0)代入y=ax2+bx+1,得到 ![]() ,解得
,解得 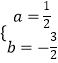 ,
,
∴二次函数的解析式为y= ![]() x2﹣
x2﹣ ![]() x+1.
x+1.
所以答案是y=﹣ ![]() x+1,y=
x+1,y= ![]() x2﹣
x2﹣ ![]() x+1.
x+1.
⑵由已知二次函数y=ax2+bx+m的图象的图象经过A、B两点,得到
![]() ,
,
解得 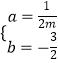 ,
,
∴二次函数的解析式为y= ![]() x2﹣
x2﹣ ![]() x+m.
x+m.
所以答案是y= ![]() x2﹣
x2﹣ ![]() x+m.
x+m.
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法).

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答下列问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | m | 0.25 |
四 | 80.5~90.5 | 80 | n |
五 | 90.5~100.5 | 24 | 0.12 |
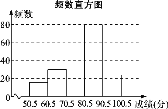
(1)写出表中:m,n,此样本中成绩的中位数落在第几组内;
(2)补全频数直方图;
(3)若成绩超过80分为优秀,该校八年级学生中汉字听写能力优秀的约有多少人?