题目内容
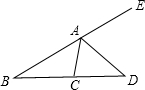如下图，在△ABC中，AD平分外角∠CAE，∠B=30°，∠CAD=65°，则∠ACD等于
- A.50°
- B.65°
- C.80°
- D.95°
C
分析：利用平分线的性质，三角形的内角和定理以及外角的性质计算．
解答：由题意可得，∠CAE=130°，
∴∠BAC=50°，
∴∠ACD=∠B+∠BAC=30°+50°=80°．
故选C．
点评：此题主要考查角平分线的性质，三角形的内角和定理以及外角的性质．
分析：利用平分线的性质，三角形的内角和定理以及外角的性质计算．
解答：由题意可得，∠CAE=130°，
∴∠BAC=50°，
∴∠ACD=∠B+∠BAC=30°+50°=80°．
故选C．
点评：此题主要考查角平分线的性质，三角形的内角和定理以及外角的性质．
练习册系列答案
相关题目
2、如下图，在△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线，若AD=2cm，则CD=
25、如下图，在△ABC中，AD平分外角∠CAE，∠B=30°，∠CAD=65°，则∠ACD等于（ ）
16、如下图，在△ABC中，AB=8，BC=6，AC的垂直平分线MN交AB、AC于点M、N．则△BCM的周长为
18、已知如下图，在△ABC中，AB=AC，AD⊥BC，垂足为D，则图中相等的线段还有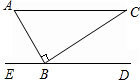
如下图，在△ABC中，∠C=30°，∠ABC=90°，AC∥BD，则∠ABD=